Concepto De Plano Cartesiano En Matemáticas: Definición Y Aplicaciones

El plano cartesiano es una herramienta fundamental en el campo de las matemáticas que permite representar gráficamente relaciones numéricas y funciones. Consiste en un sistema de referencia bidimensional formado por dos ejes perpendiculares, el eje x (horizontal) y el eje y (vertical), que se intersectan en un punto denominado origen. Esta estructura facilita la visualización y el análisis de datos, así como la resolución de ecuaciones.

En este artículo, exploraremos en profundidad el concepto de plano cartesiano, sus características, y su importancia en diversas aplicaciones matemáticas. Acompáñanos a desentrañar los principios que rigen esta poderosa herramienta y descubre cómo puede transformar tu comprensión de las matemáticas.

Comprendiendo el Plano Cartesiano: Definición, Ejes y Aplicaciones en Matemáticas

El plano cartesiano es una herramienta fundamental en matemáticas que permite representar gráficamente relaciones entre números. Este sistema de coordenadas, ideado por el filósofo y matemático René Descartes, se basa en la intersección de dos líneas perpendiculares, denominadas ejes. A continuación, se detallan los componentes más relevantes del plano cartesiano.

• Ejes del Plano Cartesiano: El plano cartesiano está compuesto por dos ejes:
• Eje horizontal (eje X): Representa la variable independiente y se extiende de izquierda a derecha.
• Eje vertical (eje Y): Representa la variable dependiente y se extiende de abajo hacia arriba.

La intersección de estos ejes forma un punto denominado origen, que se designa como (0,0). Cada punto en el plano cartesiano se identifica con un par ordenado de coordenadas (X, Y), donde X indica la posición sobre el eje horizontal y Y sobre el eje vertical.

• Cuadrantes del Plano Cartesiano: El plano se divide en cuatro cuadrantes, cada uno con características específicas:
• Primer cuadrante (I): X > 0, Y > 0; ambos valores son positivos.
• Segundo cuadrante (II): X 0; valor negativo para X y positivo para Y.
• Tercer cuadrante (III): X < 0, Y < 0; ambos valores son negativos.
• Cuarto cuadrante (IV): X > 0, Y < 0; valor positivo para X y negativo para Y.

Aplicaciones del Plano Cartesiano en Matemáticas: Este sistema no solo es útil para representar puntos, sino que también tiene diversas aplicaciones:

• Geometría: Facilita la representación de figuras geométricas, permitiendo el cálculo de distancias y áreas.
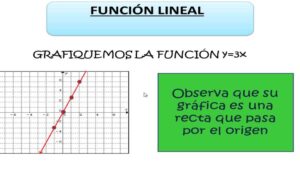
• Funciones: Permite graficar funciones matemáticas, proporcionando una visualización clara de su comportamiento.
• Estadística: Se utiliza en la representación de datos mediante gráficos, como histogramas o diagramas de dispersión.
• Física: Es crucial en la representación de movimientos y fuerzas en un sistema de coordenadas.

En conclusión, el plano cartesiano es un componente esencial en diversas ramas de las matemáticas y ciencias aplicadas. Su estructura organizada y su capacidad para representar información compleja lo convierten en una herramienta indispensable para el análisis y la resolución de problemas.

Plano Cartesiano – Concepto

PLANO CARTESIANO Super facil

¿Qué es el plano cartesiano en matemáticas?

El plano cartesiano es un sistema de coordenadas que permite representar gráficamente puntos en un espacio bidimensional. Se compone de dos líneas perpendiculares que se cruzan en un punto llamado origen, que se denota como (0,0). Estas dos líneas son el eje X (horizontal) y el eje Y (vertical).

En el plano cartesiano, cada punto se representa mediante un par ordenado de números, conocido como coordenadas. La primera coordenada indica la posición en el eje X y la segunda en el eje Y. Por ejemplo, el punto A (3, 2) se encuentra a 3 unidades a la derecha del origen y 2 unidades hacia arriba.

El plano cartesiano se divide en cuadrantes:
1. Primer cuadrante: donde ambos valores de las coordenadas son positivos.
2. Segundo cuadrante: donde la coordenada X es negativa y la Y es positiva.
3. Tercer cuadrante: donde ambas coordenadas son negativas.
4. Cuarto cuadrante: donde la coordenada X es positiva y la Y es negativa.

Este sistema es fundamental en matemáticas porque permite visualizar relaciones entre variables, resolver ecuaciones y analizar funciones de manera más efectiva. El uso del plano cartesiano es esencial en diversas áreas de la matemática y sus aplicaciones, como la geometría, el álgebra y el cálculo.

¿Qué es un plano cartesiano en matemáticas según Wikipedia?

Un plano cartesiano es un sistema de coordenadas bidimensional que permite representar de manera gráfica relaciones entre dos variables. Este plano se forma mediante la intersección de dos ejes perpendiculares: el eje horizontal (eje X) y el eje vertical (eje Y). Cada punto en el plano se identifica mediante un par ordenado de números, conocido como coordenadas, que indican su posición respecto a estos ejes.

El punto donde se cruzan los ejes se llama origen y se denota como (0, 0). El plano cartesiano es fundamental en matemáticas y se utiliza en diversas áreas, como la geometría, el álgebra y el cálculo, para facilitar el análisis y la visualización de funciones y relaciones numéricas.

¿Qué es el plano cartesiano y quién lo creó?

El plano cartesiano es un sistema de coordenadas que permite representar puntos en un espacio bidimensional utilizando dos ejes perpendiculares. Estos ejes, denominados eje X (horizontal) y eje Y (vertical), se cruzan en un punto llamado origen, que se denota como (0,0). Cada punto en el plano se identifica mediante un par ordenado de números, donde el primer número indica la posición sobre el eje X y el segundo número indica la posición sobre el eje Y.

Este concepto fue creado por el filósofo y matemático francés René Descartes en el siglo XVII. Su obra «La Géométrie» introdujo este sistema, lo que permitió establecer una relación entre el álgebra y la geometría, facilitando la representación gráfica de ecuaciones matemáticas.

De manera resumida, el plano cartesiano es fundamental en matemáticas y diversas disciplinas, ya que proporciona un marco visual para estudiar relaciones y movimientos en dos dimensiones.

¿Cuáles son los componentes del plano cartesiano?

El plano cartesiano es un sistema que permite representar gráficamente puntos y figuras en un espacio bidimensional. Sus componentes son fundamentales para la comprensión de este sistema. A continuación se detallan sus principales elementos:

1. Ejes: El plano cartesiano está formado por dos líneas perpendiculares llamadas ejes. Estos son:
– Eje X: Representa la coordenada horizontal.
– Eje Y: Representa la coordenada vertical.

2. Origen: Es el punto de intersección de los ejes X e Y, denotado como (0,0). Es el punto de referencia desde el cual se miden todas las demás coordenadas.

3. Cuadrantes: El plano se divide en cuatro partes llamadas cuadrantes, numerados en sentido antihorario a partir del cuadrante superior derecho:
– Cuadrante I: Donde ambas coordenadas son positivas.
– Cuadrante II: Donde la coordenada X es negativa y la Y es positiva.
– Cuadrante III: Donde ambas coordenadas son negativas.
– Cuadrante IV: Donde la coordenada X es positiva y la Y es negativa.

4. Puntos: Cada punto en el plano cartesiano se representa mediante un par ordenado de números (x, y), donde x es la coordenada en el eje X y y es la coordenada en el eje Y.

5. Escala: Es la medida utilizada para asignar un valor a las unidades en los ejes, permitiendo representar correctamente las distancias y proporciones en el plano.

Conocer estos componentes es esencial para trabajar con el plano cartesiano y realizar gráficas de funciones matemáticas, así como para la resolución de problemas en geometría y álgebra.

Preguntas Frecuentes

¿Qué es el plano cartesiano y cuáles son sus componentes principales?

El plano cartesiano es un sistema de representación gráfica que permite ubicar puntos en dos dimensiones mediante pares de números. Sus componentes principales son:

1. Ejes: Dos líneas perpendiculares, el eje X (horizontal) y el eje Y (vertical).
2. Origen: El punto donde se intersectan los ejes, representado como (0,0).
3. Coordenadas: Los pares ordenados (x, y) que indican la posición de un punto en el plano.

¿Cómo se utilizan las coordenadas en el plano cartesiano?

Las coordenadas en el plano cartesiano se representan mediante un par de valores (x, y), donde x indica la posición horizontal y y la posición vertical. Estos valores permiten ubicar puntos en un sistema de referencia compuesto por dos ejes perpendiculares: el eje X (horizontal) y el eje Y (vertical). Al utilizar estas coordenadas, es posible realizar análisis geométricos, graficar funciones y resolver problemas matemáticos.

¿Cuál es la importancia del plano cartesiano en la representación gráfica de funciones?

El plano cartesiano es fundamental en la representación gráfica de funciones porque permite visualizar la relación entre las variables de una función. Al asignar coordenadas a cada punto en el plano, se facilita el análisis de comportamientos, tendencias y intersecciones de la función. Esto ayuda a interpretar de manera más clara los datos y a realizar predicciones sobre el comportamiento futuro de la función.

¿Qué diferencias existen entre el plano cartesiano y otros sistemas de coordenadas?

El plano cartesiano utiliza un sistema de coordenadas rectangulares, donde se representan puntos mediante dos ejes perpendiculares (x, y). En cambio, otros sistemas de coordenadas, como el sistema polar, utilizan un ángulo y una distancia desde un punto de origen para definir la posición de un punto. Además, el plano cartesiano es más intuitivo para representar relaciones lineales, mientras que sistemas como el sistema cilíndrico o sistema esférico son más útiles en contextos tridimensionales y aplicaciones específicas en física y geometría.

En conclusión, el plano cartesiano es una herramienta fundamental en las matemáticas que permite la representación y análisis de datos en dos dimensiones. Su comprensión abre la puerta a un sinfín de aplicaciones prácticas y teóricas. Te invitamos a compartir este contenido y seguir explorando más conceptos y definiciones.