En el ámbito de las matemáticas, el cociente es un concepto fundamental que juega un papel crucial en diversas áreas como la aritmética, el álgebra y la teoría de números. Se define como el resultado de dividir un número entre otro, lo que permite analizar relaciones numéricas y resolver problemas complejos. A través de esta operación, se puede entender mejor la distribución de cantidades y realizar cálculos precisos en contextos tanto teóricos como prácticos. En este artículo, exploraremos en profundidad el concepto de cociente, sus propiedades y aplicaciones, así como su relevancia en el desarrollo del pensamiento matemático.
Contenido
- 1 Entendiendo el Cociente: Definición y Aplicaciones en Matemáticas
- 2 Cuál es el cociente en una división – Aprender a dividir
- 3 Act. 10 – ¿Qué es un cociente?
- 4 ¿Cuál es el significado del cociente en matemáticas?
- 5 ¿Qué se entiende por cociente en estadística?
- 6 ¿Qué significa cociente en matemáticas según Wikipedia?
- 7 ¿Cómo se calcula el cociente?
- 8 Preguntas Frecuentes
Entendiendo el Cociente: Definición y Aplicaciones en Matemáticas
El cociente es un concepto fundamental dentro de las matemáticas, que se refiere al resultado de la división de un número entre otro. Este término se utiliza en diversas áreas y aplicaciones, desde la aritmética básica hasta el cálculo avanzado. A continuación, se presenta una definición más detallada y sus aplicaciones en diferentes contextos matemáticos.
Definición del Cociente
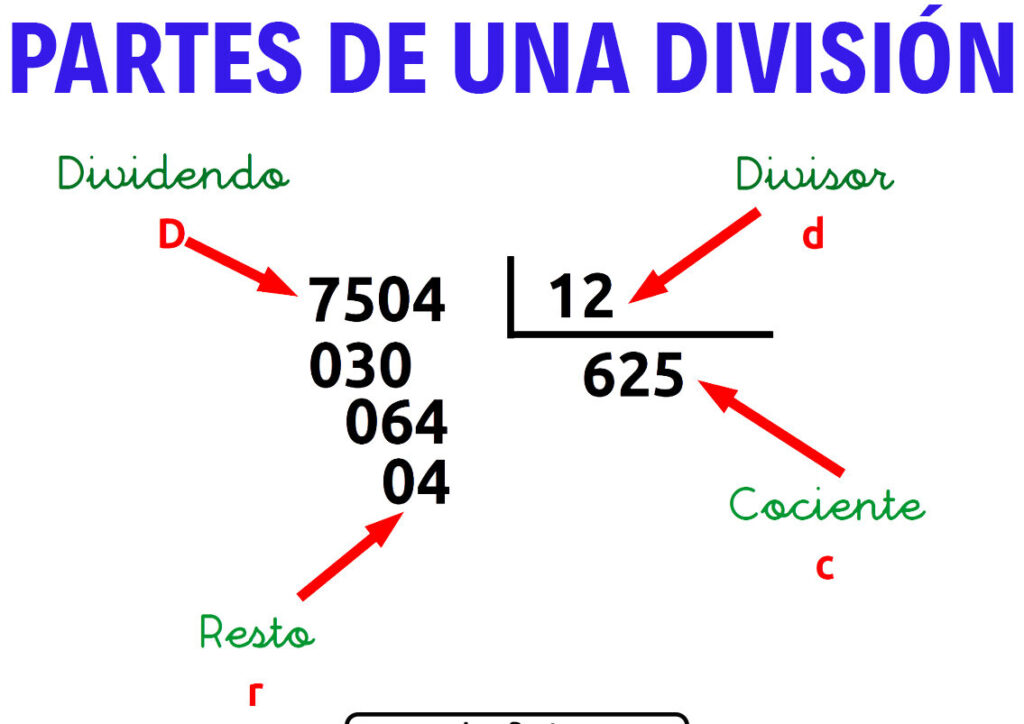
El cociente se define como el número que resulta al dividir un número (llamado dividendo) por otro (denominado divisor). Matemáticamente, se expresa de la siguiente manera:
Donde:
- Dividendo: Es el número que se va a dividir.
- Divisor: Es el número entre el cual se divide el dividendo.
Propiedades del Cociente
El cociente presenta ciertas propiedades que son importantes en el estudio de las matemáticas:
- Conmutatividad: La operación de división no es conmutativa, es decir, A ÷ B no es igual a B ÷ A.
- Asociatividad: La división tampoco es asociativa, lo que significa que (A ÷ B) ÷ C no es igual a A ÷ (B ÷ C).
- División por cero: No se puede dividir un número entre cero, ya que esto no tiene sentido matemático.
Aplicaciones del Cociente en Matemáticas
El cociente tiene múltiples aplicaciones en diferentes ramas de las matemáticas. Algunas de ellas incluyen:
- Aritmética: En operaciones básicas, el cociente se utiliza para resolver problemas cotidianos, como repartir cantidades equitativamente.
- Álgebra: Se emplea en la simplificación de fracciones y en la resolución de ecuaciones que involucran divisiones.
- Cálculo: En el cálculo diferencial, el cociente se utiliza en el concepto de derivadas, donde se evalúa la razón de cambio de una función respecto a otra.
- Estadística: En el análisis estadístico, el cociente se aplica para calcular promedios y tasas, permitiendo comparar diferentes conjuntos de datos.
- Geometría: En la geometría, se usa para determinar proporciones en figuras y en el cálculo de áreas y volúmenes en relación a dimensiones específicas.
Además, el cociente se encuentra presente en diversas fórmulas matemáticas y teoremas que son esenciales para el desarrollo de temas más avanzados. Por ejemplo, en álgebra, la regla del cociente se utiliza para derivar funciones que son el cociente de dos funciones.
En conclusión, el cociente es un concepto central en matemáticas que facilita la comprensión y resolución de problemas en diversas disciplinas. Su importancia se manifiesta en su amplia gama de aplicaciones y en las herramientas matemáticas que permite desarrollar.
Cuál es el cociente en una división – Aprender a dividir
Act. 10 – ¿Qué es un cociente?
¿Cuál es el significado del cociente en matemáticas?
En matemáticas, el cociente es el resultado de una división entre dos números. Se representa comúnmente como a ÷ b, donde a es el dividendo y b es el divisor. El cociente se denota frecuentemente por la letra q en las ecuaciones.
Definición: Si tenemos dos números, a y b (con b diferente de cero), el cociente se define como:
q = a ÷ b
Esto significa que el cociente indica cuántas veces el divisor b puede ser contenido en el dividendo a. Por ejemplo, si dividimos 10 entre 2, el cociente es 5, ya que 2 cabe 5 veces en 10.
En contextos más avanzados, el cociente también puede referirse a la relación entre dos cantidades en términos de proporciones o fracciones. En resumen, el cociente es una noción fundamental en el campo de las matemáticas que permite entender la división y las relaciones numéricas.
¿Qué se entiende por cociente en estadística?
En estadística, el término cociente se refiere a la relación o comparación entre dos cantidades. Se obtiene al dividir una cantidad entre otra, lo que permite analizar y entender cómo se relacionan esas dos cantidades.
Un cociente puede ser utilizado en diversas aplicaciones estadísticas, como en el cálculo de tasas, índices y proporciones. Por ejemplo, si se desea calcular el cociente de dos grupos en un estudio, se podría dividir el número de elementos en un grupo por el número de elementos en otro grupo. Este tipo de análisis ayuda a identificar diferencias o similitudes entre los grupos evaluados.
Es importante destacar que el cociente también puede proporcionar información sobre tendencias y patrones dentro de un conjunto de datos, lo que resulta fundamental para la interpretación de resultados en investigaciones estadísticas.
¿Qué significa cociente en matemáticas según Wikipedia?
En matemáticas, el término cociente se refiere al resultado de una división. Específicamente, cuando se divide un número (llamado dividendo) por otro número (llamado divisor), el resultado que obtenemos es el cociente.
Por ejemplo, en la operación ( a div b = c ), el número ( c ) es el cociente, donde ( a ) es el dividendo y ( b ) es el divisor. Es importante señalar que el divisor no puede ser cero, ya que la división por cero no está definida.
El cociente puede ser un número entero, un número decimal o incluso una fracción, dependiendo de los valores del dividendo y el divisor.
¿Cómo se calcula el cociente?
El cociente es el resultado de una división entre dos números. Para calcularlo, se siguen los siguientes pasos:
1. Identificar los números: Se necesita un dividendo (el número que se va a dividir) y un divisor (el número por el cual se divide).
2. Realizar la división: Se divide el dividendo entre el divisor. Esto se puede hacer utilizando calculadoras, operaciones matemáticas manuales o algoritmos de división.
3. Interpretar el resultado: El resultado de la división es el cociente. Si hay un residuo (es decir, si el dividendo no se puede dividir exactamente por el divisor), el cociente puede expresarse como un número entero más una fracción o decimal que represente el residuo.
Por ejemplo, al dividir 10 entre 3:
- El dividendo es 10.
- El divisor es 3.
- El cociente sería 3 con un residuo de 1, lo que también se puede expresar como 3.33 si se convierte a decimal.
En resumen, el cociente se calcula dividiendo el dividendo por el divisor y puede ser representado en diferentes formas según los resultados de la operación.
Preguntas Frecuentes
¿Qué es el cociente en matemáticas y cómo se calcula?
El cociente en matemáticas es el resultado de una división. Se calcula dividiendo el dividendo entre el divisor. Por ejemplo, en la operación 10 ÷ 2, el cociente es 5.
¿Cuál es la diferencia entre cociente y residuo en una división?
En una división, el cociente es el resultado de contar cuántas veces cabe el divisor en el dividendo, mientras que el residuo es lo que queda después de realizar esa división, es decir, la cantidad que no se puede dividir más por el divisor.
¿En qué contextos se utiliza el concepto de cociente en matemáticas?
El concepto de cociente en matemáticas se utiliza principalmente en los siguientes contextos:
1. División: Representa el resultado de dividir un número por otro.
2. Proporciones: Se utiliza para comparar dos cantidades, indicando cuántas veces una cantidad cabe en otra.
3. Fracciones: En fracciones, el cociente es el número que resulta de dividir el numerador entre el denominador.
4. Álgebra: En el contexto de funciones, el cociente puede referirse a la relación entre dos expresiones algebraicas.
Estos contextos son fundamentales para entender cómo se relacionan las cantidades en diferentes situaciones matemáticas.
¿Cómo se aplica el cociente en problemas de la vida real?
El cociente se aplica en problemas de la vida real al determinar cuántas veces cabe una cantidad en otra. Por ejemplo, al dividir recursos entre personas para repartir equitativamente, o al calcular velocidades dividiendo la distancia recorrida entre el tiempo empleado. Esta operación permite tomar decisiones informadas y optimizar recursos en diversas situaciones cotidianas.
En conclusión, el cociente es un concepto fundamental en matemáticas que permite entender la relación entre dos cantidades a través de la división. Su comprensión es esencial para el estudio de operaciones más complejas. Te invitamos a compartir este contenido y a seguir explorando más conceptos matemáticos en nuestro sitio.