Concepto De Lema En Matemáticas: Clave Para Resolver Problemas Complejos

El concepto de lema en matemáticas es fundamental para la comprensión y desarrollo de diversas teorías dentro de esta disciplina. Un lema se define como un enunciado auxiliar que se utiliza para demostrar un teorema más complejo. Estos lemas son esenciales, ya que permiten simplificar la argumentación matemática y facilitar la resolución de problemas.

La importancia de los lemas radica en su capacidad para desglosar una demostración en pasos más manejables, lo que contribuye a un análisis más claro y estructurado. A lo largo de este artículo, exploraremos en profundidad el papel de los lemas en las matemáticas, su relación con los teoremas y ejemplos ilustrativos que destacan su función. Te invitamos a continuar leyendo para descubrir más sobre este fascinante aspecto de la matemática.

Entendiendo el Lema en Matemáticas: Definición, Importancia y Ejemplos Prácticos

El lema en matemáticas es una herramienta fundamental en el desarrollo de teoremas y resultados dentro de este campo. Se define como una proposición o afirmación que, aunque puede no ser de interés por sí misma, es esencial para demostrar otros teoremas más significativos. A continuación, se exploran su definición, importancia y se presentan ejemplos prácticos.

Definición del lema: Se entiende como un pequeño resultado que se utiliza como paso intermedio en una demostración más extensa. Un lema no tiene la misma relevancia que un teorema, pero es crucial para establecer el fundamento o la estructura lógica sobre la cual se construyen argumentos más complejos.

Importancia de los lemas: En la matemática avanzada, los lemas juegan un papel importante porque:

• Facilitan la deducción lógica: Al dividir un problema más grande en partes más manejables, los lemas permiten a los matemáticos enfocarse en aspectos específicos sin perder la visión general.
• Clarifican la argumentación: Un lema puede simplificar la comprensión de un teorema al agrupar propiedades relacionadas en una afirmación más sencilla.
• Proporcionan estructura: Los lemas son útiles para organizar un trabajo matemático, sirviendo como escalones hacia la conclusión deseada.
• Aumentan la eficiencia: Evitan la redundancia al permitir reutilizar resultados conocidos en diversas demostraciones.

Ejemplos prácticos de lemas: A menudo, los lemas se utilizan en distintas ramas de las matemáticas, tales como la teoría de números, álgebra y análisis. Algunos ejemplos incluyen:

• Lema de Zorn: Este lema establece que si cada cadena (subconjunto totalmente ordenado) de un conjunto parcialmente ordenado tiene una cota superior, entonces el conjunto tiene al menos un elemento maximal. Es fundamental en teoría de conjuntos y se utiliza, por ejemplo, para demostrar la existencia de bases en espacios vectoriales.
• Lema de la contraparte: En análisis, este lema ayuda a manipular límites y derivadas, permitiendo establecer resultados sobre la continuidad y la diferenciabilidad de funciones.
• Lema de Euclides: Este lema establece que si un número entero divide a dos números enteros, también divide su combinación lineal. Esta propiedad es esencial en la teoría de números y se aplica en la demostración de varios teoremas importantes.

El uso de lemas en matemáticas resalta la naturaleza colaborativa y acumulativa de este campo, donde resultados aparentemente menores contribuyen a la construcción de teorías más grandes y complejas.

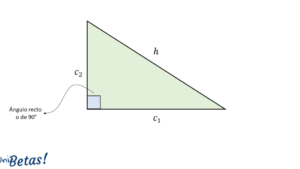
13. Qué es un LEMA y COROLARIO, Ejemplos a partir del Teorema de Pitágoras

⚠️ATENCIÓN!! Qué son? Proposición, Axioma, Postulado, Teorema, Lema y Corolario

Importancia del Lema en el Razonamiento Matemático

Definición de Razonamiento Matemático

El razonamiento matemático se refiere al proceso lógico que utiliza un individuo para deducir o inferir conclusiones a partir de un conjunto de premisas o conceptos matemáticos. Este proceso es fundamental no solo para resolver problemas, sino también para construir teorías matemáticas más complejas. El uso de lemmas juega un papel crucial dentro de este razonamiento, ya que son herramientas que permiten simplificar la demostración de teoremas más grandes y complejos.

Los lemmas proporcionan pasos intermedios que pueden hacer más manejable la resolución de problemas. Estos pasos pueden transformar una demostración que parecería inabordable en una serie de pasos más simples y comprensibles. En este sentido, el lema actúa como una especie de “puente” entre el conocimiento existente y el nuevo conocimiento que se busca establecer.

Aplicaciones de Lemmas en Diferentes Campos Matemáticos

Los lemmas son utilizados en diversas ramas de las matemáticas. A continuación, se detallan algunas de estas áreas y cómo los lemmas se integran en cada una:

• Teoría de Números: Los lemmas frecuentemente se emplean para demostrar propiedades relacionadas con la divisibilidad y los números primos. Un ejemplo clásico es el Lema de Euclides, que establece fundamentos sobre la infinitud de los números primos.
• Álgebra Abstracta: En esta área, los lemmas pueden ser utilizados para establecer resultados sobre estructuras algebraicas como grupos y anillos. Un ejemplo es el Lema de Zorn, utilizado para demostrar la existencia de bases en espacios vectoriales.
• Análisis Matemático: Aquí, los lemmas ayudan a establecer resultados sobre convergencias y límites. Un caso notable es el Lema de Bolzano-Weierstrass, que garantiza la existencia de puntos extremos en conjuntos acotados.

En cada una de estas disciplinas, los lemmas sirven como fundamentales peldaños en la construcción de argumentos coherentes y sólidos que llevan a la formulación de teoremas más amplios.

Ejemplos Notables de Lemmas en Matemáticas

A lo largo de la historia de las matemáticas, varios lemmas han adquirido una notoriedad considerable debido a su impacto en el pensamiento matemático. Algunos ejemplos notables incluyen:

• Lema de Zorn: Este lema es clave en la teoría de conjuntos y ha sido utilizado extensamente en diversas aplicaciones, incluida la demostración de que todo espacio vectorial tiene una base.
• Lema de Minkowski: Este lema es fundamental en la geometría convexa, ofreciendo condiciones necesarias para la convexidad de un conjunto.
• Lema de la Intersección: Este lema establece condiciones bajo las cuales la intersección de dos conjuntos es no vacía, lo que es útil en múltiples campos de estudio.

Estos lemmas no solo han facilitado la comprensión y resolución de problemas, sino que también han abierto nuevos caminos en la investigación matemática.

Relación entre Lemmas y Teoremas

Estructura Jerárquica en Matemáticas

Dentro de la jerarquía del conocimiento matemático, los lemmas y los teoremas ocupan lugares distintos pero interrelacionados. Mientras que un teorema es una afirmación que ha sido probada rigurosamente y tiene implicaciones significativas, un lema, por su parte, sirve como una herramienta auxiliar que ayuda a simplificar la prueba de ese teorema.

La relación entre ambos es simbiótica; los lemmas son frecuentemente necesarios para alcanzar la conclusión de un teorema. Sin la existencia de estos lemmas, muchos teoremas serían excesivamente complejos o difíciles de demostrar, lo que resalta la importancia de establecer una base sólida desde la cual se puedan edificar pruebas más elaboradas.

Proceso de Demostración: De Lemmas a Teoremas

Al emplear lemmas en la demostración de teoremas, existe un proceso sistemático que suele seguirse:

• Identificación del Problema: Se debe identificar el teorema que se desea demostrar y las dificultades que pueden surgir durante la prueba.
• Selección de Lemmas Relevantes: Posteriormente, se eligen los lemmas que faciliten la demostración del teorema en cuestión.
• Construcción de la Demostración: Finalmente, se elabora la demostración utilizando los lemmas seleccionados, asegurando que cada paso esté debidamente justificado.

Este proceso no solo hace que la demostración sea más clara, sino que también proporciona un entendimiento más profundo de cómo los diferentes conceptos matemáticos están interconectados.

Diferencias entre Lemmas, Corolarios y Proposiciones

Definición de Términos

Aunque los términos «lema», «corolario» y «proposición» pueden parecer similares, cumplen funciones distintas en la estructura del conocimiento matemático.

• Lema: Es una afirmación que se utiliza para ayudar en la demostración de un teorema. Su propósito principal es facilitar el proceso de prueba.
• Corolario: Un corolario es una afirmación que se deriva directamente de un teorema probado, generalmente con poca o ninguna necesidad de prueba adicional.
• Proposición: Una proposición es una afirmación matemática que requiere prueba, pero que no es necesariamente de la misma importancia o generalidad que un teorema.

Estas definiciones resaltan cómo cada uno de estos elementos tiene su propio rol dentro del esquema mayor de la matemática, aunque todos contribuyen al desarrollo del conocimiento.

Ejemplos para Illustrar las Diferencias

Para comprender mejor las diferencias entre estos conceptos, se pueden considerar algunos ejemplos específicos:

• Un lema como el Lema de Zorn: Este lema es utilizado para probar teoremas más avanzados, como el teorema que afirma que todo espacio vectorial tiene una base.
• Un corolario derivado de un teorema de la teoría de números: Si se prueba un teorema sobre la infinitud de los números primos, un corolario podría ser que hay infinitos primos entre cualquier par de enteros.
• Una proposición sobre series convergentes: Se puede formular varias proposiciones sobre la convergencia, que requieren prueba y que no son tan generales como los teoremas vinculados a la convergencia absoluta.

Estos ejemplos subrayan la especialización de cada uno de estos términos y su relevancia en el contexto del razonamiento matemático.

Preguntas Frecuentes

¿Qué es un lema en matemáticas y cómo se utiliza en la demostración de teoremas?

Un lema en matemáticas es una afirmación o proposición que se establece como base para ayudar a demostrar un teorema más amplio. Los lemas son importantes porque facilitan el proceso de prueba al simplificar la argumentación y permitir descomponer problemas complejos en partes más manejables. En la demostración de teoremas, los lemas se utilizan como pasos intermedios que apoyan la conclusión final, proporcionando así una estructura lógica y coherente al razonamiento matemático.

¿Cuál es la diferencia entre un lema, un teorema y una proposición en el contexto matemático?

En el contexto matemático, un teorema es una afirmación que ha sido demostrada y se considera fundamental dentro de una teoría. Una proposición es una afirmación que puede ser verdadera o falsa, pero que aún no se ha demostrado. Un lema es un resultado auxiliar utilizado para demostrar otros teoremas, generalmente de menor importancia.

¿Cómo se elige un lema adecuado en un argumento matemático?

Para elegir un lema adecuado en un argumento matemático, es fundamental identificar un resultado auxiliar que ayude a construir la prueba principal. Este lema debe ser relevante y generalizable a la situación del problema, además de ser lo suficientemente simple para demostrarlo fácilmente. Al seleccionar un lema, se busca que aporte claridad y establezca un vínculo lógico entre las premisas y la conclusión del argumento.

¿Existen ejemplos históricos importantes de lemas en matemáticas?

Sí, existen ejemplos históricos importantes de lemas en matemáticas. Un ejemplo notable es el lemade Zsigmondy’s, que establece que para ciertos enteros n y k, existen primos que no dividen a la potencia de n^k. Otro ejemplo es el lemade Fermat, que se utiliza en la demostración del Teorema de Fermat sobre números primos. Estos lemas son fundamentales en áreas como la teoría de números y tienen un gran impacto en el desarrollo de conceptos matemáticos.

En conclusión, el lema en matemáticas se erige como una herramienta esencial para estructurar y facilitar demostraciones complejas. Su comprensión es vital para el desarrollo del pensamiento lógico-matemático. Te invitamos a compartir este contenido y seguir explorando nuestros artículos para profundizar en más conceptos y definiciones fundamentales.