En el fascinante mundo de la geometría, el ángulo central se erige como un concepto fundamental que conecta puntos, arcos y circunferencias. Definido como aquel ángulo cuyo vértice se encuentra en el centro de un círculo, y cuyos lados son segmentos que se extienden hasta la circunferencia, resulta crucial para entender fenómenos más complejos en matemáticas.
A medida que exploramos este concepto, descubriremos no solo su definición precisa, sino también su aplicación en diversas áreas, desde la trigonometría hasta la física. Sigamos adelante para desentrañar los secretos y las propiedades del ángulo central, una pieza clave en el rompecabezas geométrico que nos rodea.
Contenido
- 1 Definición y Significado del Ángulo Central en Matemáticas: Fundamentos y Aplicaciones
- 2 ANGULOS ENTRE PARALELAS Y UNA TRANSVERSAL (EJERCICIOS) Super facil – Para principiantes
- 3 Matemática Básica – Angulos y Arcos en Circunferencia
- 4 ¿Qué significa ángulo central?
- 5 ¿Cómo se representa un ángulo central?
- 6 ¿Qué se entiende por ángulo central en una figura regular?
- 7 ¿Qué se entiende por un ángulo central recto?
- 8 Preguntas Frecuentes
Definición y Significado del Ángulo Central en Matemáticas: Fundamentos y Aplicaciones
El ángulo central es un concepto fundamental en la geometría que se refiere a un tipo específico de ángulo formado en el centro de un círculo. Este ángulo está delimitado por dos radios, que son segmentos de línea que conectan el centro del círculo con dos puntos en su circunferencia. La medida del ángulo central está directamente relacionada con la longitud del arco que subtende en la circunferencia.
La definición matemática del ángulo central se establece formalmente de la siguiente manera:
1. Definición: Un ángulo central es aquel cuyo vértice coincide con el centro de un círculo y cuyos lados son radios del círculo.
2. Medición: La medida del ángulo central, generalmente expresada en grados, es igual a la medida del arco que abarca en la circunferencia. Es decir, un ángulo central de 60° subtenderá un arco que tiene una longitud equivalente a 1/6 de la circunferencia total.
Las propiedades del ángulo central son fundamentales para la comprensión de otros conceptos geométricos. Entre las más relevantes, se pueden mencionar:
- Relación con el arco: Como se mencionó anteriormente, la medida del ángulo central es igual a la medida del arco que subtende. Esta propiedad permite establecer relaciones directas entre diferentes elementos del círculo.
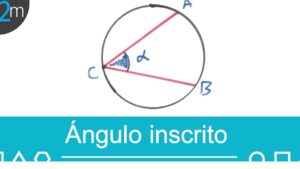
- Ángulos inscriptos: Un ángulo inscripto es aquel cuyo vértice está en la circunferencia y cuyas lados son cuerdas del círculo. La relación entre un ángulo central y un ángulo inscripto que subtenden el mismo arco es que el ángulo inscripto mide la mitad del ángulo central.
- Cálculo de áreas: El ángulo central también juega un papel esencial en el cálculo de áreas de sectores circulares, que son las porciones del círculo delimitadas por dos radios y el arco correspondiente.
Las aplicaciones del ángulo central son diversas y se extienden a múltiples campos de estudio:
- Diseño Gráfico: En el diseño gráfico, los ángulos centrales se utilizan para crear proporciones perfectas y simetrías en composiciones circulares.
- Ingeniería: En ingeniería mecánica, se aplican ángulos centrales al diseñar engranajes y sistemas de poleas, donde las fuerzas aplicadas dependen de ángulos precisos.
- Arquitectura: En arquitectura, la disposición de elementos circulares en estructuras, como cúpulas, requiere un entendimiento sólido de los ángulos centrales para garantizar la estabilidad y la estética.
- Astrofísica: En astrofísica, los ángulos centrales son importantes para el estudio de órbitas planetarias y la observación de cuerpos celestes desde un punto central.
En resumen, el ángulo central no solo es un concepto geométrico básico, sino que también es una herramienta valiosa en múltiples disciplinas, mostrando su relevancia en aplicaciones prácticas y teóricas. Su estudio permite una mejor comprensión de la geometría del círculo y sus propiedades asociadas.
ANGULOS ENTRE PARALELAS Y UNA TRANSVERSAL (EJERCICIOS) Super facil – Para principiantes
Matemática Básica – Angulos y Arcos en Circunferencia
¿Qué significa ángulo central?
Un ángulo central es un concepto fundamental en la geometría, que se refiere a un ángulo cuyo vértice se encuentra en el centro de un círculo y cuyos lados son radios de dicho círculo. Este ángulo abarca una porción del círculo y su medida se expresa en grados o radianes.
La medida de un ángulo central es igual a la medida del arco que intercepta en el círculo. Esto significa que si un ángulo central mide, por ejemplo, 60 grados, el arco correspondiente también tendrá una longitud que equivale a 60 grados en el círculo.
En resumen, un ángulo central se caracteriza por:
1. Su vértice está en el centro del círculo.
2. Sus lados son radios del círculo.
3. Su medida es igual a la medida del arco que intercepta.
Este concepto es esencial para entender las propiedades de los círculos y su relación con los ángulos en la geometría.
¿Cómo se representa un ángulo central?
Un ángulo central es un ángulo cuyos vértices se encuentran en el centro de un círculo, y sus lados son segmentos de radio que se extienden hasta la circunferencia del círculo.
Para representar un ángulo central, se suelen seguir los siguientes pasos:
1. Dibuja un círculo: Utiliza un compás o trazos a mano alzada para crear una circunferencia.
2. Marca el centro: Identifica y señala el punto central del círculo, denotándolo comúnmente con la letra «O».
3. Dibuja dos radios: Traza dos segmentos de línea desde el centro «O» hasta la circunferencia, eligiendo dos puntos en la circunferencia llamados «A» y «B». Estos segmentos (OA y OB) son los lados del ángulo.
4. Indica el ángulo: El ángulo formado por los segmentos OA y OB se representa como ∠AOB. Este símbolo indica que el vértice está en «O» y que los lados del ángulo son los segmentos OA y OB.
En resumen, un ángulo central se representa claramente al visualizar un círculo con su centro marcado y los dos radios que conforman el ángulo visible en la circunferencia.
¿Qué se entiende por ángulo central en una figura regular?
Un ángulo central en una figura regular es un ángulo cuyo vértice se encuentra en el centro de la figura y cuyos lados son radios que conectan el centro con dos puntos distintos en el contorno de la figura. Este tipo de ángulo permite medir la separación angular entre esos dos puntos en relación al centro.
En el caso de figuras regulares, como un polígono regular (por ejemplo, un triángulo equilátero o un cuadrado), todos los ángulos centrales son iguales y se pueden calcular dividiendo el total de los 360 grados del círculo entre el número de lados del polígono. Así, por ejemplo, en un hexágono regular, cada ángulo central mide 60 grados, ya que 360 grados / 6 lados = 60 grados.
Este concepto es fundamental en la geometría, ya que proporciona una base para entender las propiedades de las figuras regulares y su simetría.
¿Qué se entiende por un ángulo central recto?
Un ángulo central recto es un tipo específico de ángulo en el contexto de la geometría. Se define como un ángulo cuyo vértice se encuentra en el centro de un círculo y cuyos lados son radios del mismo círculo.
La medida de un ángulo central recto es de 90 grados, lo que significa que forma un cuadrante del círculo. Este tipo de ángulo es fundamental en diversas aplicaciones, incluyendo la trigonometría y la construcción de figuras geométricas.
Además, los ángulos centrales son importantes porque su medida está directamente relacionada con los arcos que delimitan. En el caso de un ángulo central recto, el arco correspondiente abarca exactamente un cuarto de la circunferencia del círculo.
Preguntas Frecuentes
¿Qué es un ángulo central en matemáticas y cómo se define?
Un ángulo central en matemáticas es un ángulo cuyo vértice se encuentra en el centro de un círculo y sus lados son radios del mismo. Se define como el ángulo formado por dos radios que delimitan un arco en la circunferencia del círculo. Su medida se expresa en grados o radianes y es igual a la medida del arco que abarca.
¿Cuál es la relación entre el ángulo central y el arco de un círculo?
La relación entre el ángulo central y el arco de un círculo es que el ángulo central, cuyo vértice se encuentra en el centro del círculo, determina la medida del arco que subtende. Es decir, el medida del arco es directamente proporcional a la medida del ángulo central, expresándose en grados o radianes.
¿Cómo se calcula un ángulo central en función del radio de un círculo?
El ángulo central de un círculo se calcula en función del longitud del arco y el radio del círculo. La fórmula es:
θ = s / r
donde θ es el ángulo central en radianes, s es la longitud del arco y r es el radio del círculo. Esta relación muestra cómo el tamaño del ángulo depende de la longitud del arco que abarca.
¿Cuáles son las propiedades más importantes del ángulo central en geometría?
El ángulo central en geometría tiene varias propiedades importantes:
1. Medida: La medida de un ángulo central es igual a la medida del arco que intercepta en el círculo.
2. Relación con el círculo: El ángulo central se forma en el centro del círculo, lo que lo distingue de otros ángulos que pueden formarse en el perímetro.
3. Ángulos iguales: Si hay dos ángulos centrales que interceptan el mismo arco, son iguales en medida.
Estas propiedades son fundamentales para entender el comportamiento de los ángulos en la geometría circular.
En conclusión, el ángulo central es un concepto fundamental en matemáticas que permite comprender mejor la relación entre el círculo y sus propiedades. Para ampliar tus conocimientos, te invitamos a compartir este artículo y seguir explorando más conceptos matemáticos que enriquecerán tu aprendizaje. ¡No te lo pierdas!