Concepto De Cálculo Integral Y Sus Aplicaciones En La Ciencia Y La Ingeniería

El cálculo integral es una de las dos ramas fundamentales del cálculo, centrada en la acumulación de cantidades y el análisis de áreas bajo curvas. Se define como el proceso matemático que permite calcular la integral de una función, proporcionando herramientas para resolver problemas que implican el área, el volumen y otros conceptos relacionados con la acumulación.

Las aplicaciones del cálculo integral son vastas y variadas, extendiéndose a campos como la física, la ingeniería, la economía y la biología. Desde la determinación de la trayectoria de un objeto en movimiento hasta la evaluación del costo total en funciones económicas, el cálculo integral se convierte en una herramienta esencial para modelar y comprender fenómenos complejos en el mundo real.

A medida que profundicemos en este artículo, exploraremos más a fondo el concepto de cálculo integral y sus diversas aplicaciones en distintos ámbitos. Invitamos al lector a continuar leyendo para descubrir su relevancia y utilidad en el estudio de diversas disciplinas.

Introducción al Cálculo Integral: Definición, Principios Fundamentales y Aplicaciones en Diversos Campos

El cálculo integral es una de las ramas fundamentales del cálculo, enfocado en la noción de integración, que permite calcular el área bajo una curva, volúmenes de sólidos de revolución y resolver problemas relacionados con tasas de acumulación. A continuación, se presentan su definición, principios y aplicaciones en diversos campos.

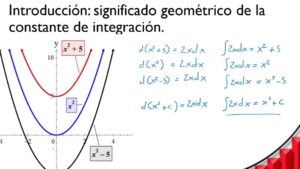
Definición: El cálculo integral se puede definir como el proceso de encontrar una función que representa la acumulación de cantidades a partir de su tasa de cambio. Formalmente, la integral de una función f(x) se representa como ∫f(x)dx, donde el resultado se conoce como la primitiva o antiderivada de f(x).

Principios Fundamentales: Los principios del cálculo integral son los siguientes:

• Teorema Fundamental del Cálculo: Este teorema establece la relación entre las derivadas y las integrales. Afirma que si F es una antiderivada de f en un intervalo [a, b], entonces:
  • ∫_a^b f(x)dx = F(b) – F(a)
• Linealidad de la Integral: Establece que la integral de una suma de funciones es igual a la suma de las integrales, así como también permite extraer constantes fuera del signo integral.
• Propiedades de la Integral: La integral definida es aditiva en intervalos y tiene propiedades asociativas, lo que permite un análisis más flexible de las funciones integradas.

Aplicaciones en Diversos Campos: El cálculo integral tiene amplias aplicaciones en múltiples disciplinas, tales como:

• Física</: En la física, se utiliza para calcular desplazamientos, áreas bajo gráficas de velocidad versus tiempo, y la energía acumulada en sistemas dinámicos.
• Ingeniería: Se aplica en el diseño y análisis de estructuras, donde el cálculo de momentos y fuerzas implica el uso de integrales para determinar cargas a lo largo de una viga o superficie.
• Economía: En economía, se usa para determinar costos totales, ingresos y beneficios a partir de funciones de costes marginales y de ingresos.
• Biología: En biología, se puede utilizar para modelar la población dinámica y calcular la biomasa en ecosistemas, considerando las tasas de crecimiento y muerte de organismos.
• Estadística: En estadística, se aplica en la teoría de probabilidades para encontrar distribuciones acumulativas y valores esperados, integrando funciones de densidad.

Las aplicaciones del cálculo integral demuestran su importancia y versatilidad en el análisis matemático de fenómenos complejos y su contribución al avance del conocimiento en diversas áreas.

Clase #1 de Integrales: Inmediatas y Cambio de Variable

Integrales definidas | Ejemplo 3

Historia del Cálculo Integral

Orígenes del Cálculo Integral

El cálculo integral tiene sus raíces en los trabajos de matemáticos como Isaac Newton y Gottfried Wilhelm Leibniz, quienes, independientemente, desarrollaron las bases del cálculo en el siglo XVII. Este desarrollo fue un hito en la matemática, ya que permitió establecer métodos para calcular áreas bajo curvas y resolver problemas complejos que antes eran inalcanzables.

A lo largo de la historia, se han encontrado vestigios del cálculo en civilizaciones antiguas, como los egipcios y babilonios, que utilizaron métodos rudimentarios para calcular áreas. Sin embargo, el verdadero formalismo del cálculo llegó a consolidarse con el trabajo de Newton y Leibniz, quienes introdujeron, respectivamente, la notación de la integral y los principios de su aplicación.

Evolución del Cálculo Integral

Desde sus descubrimientos iniciales, el cálculo integral ha evolucionado significativamente. En el siglo XVIII, matemáticos como Leonhard Euler y Augustin-Louis Cauchy elaboraron teorías más completas y precisas sobre las integrales, ampliando su campo de aplicación. Se introdujeron conceptos fundamentales como las funciones continuas y las series infinitas.

El desarrollo de la teoría de límites y la convergencia en el siglo XIX también jugó un papel crucial en la comprensión del cálculo integral. Esto permitió establecer un marco riguroso que abarcaba tanto el análisis de integrales definidas como indefinidas, cimentando así su lugar en la matemática moderna.

Principios Fundamentales del Cálculo Integral

Teorema Fundamental del Cálculo

Uno de los pilares del cálculo integral es el Teorema Fundamental del Cálculo, que conecta el proceso de integración con el de diferenciación. Este teorema se divide en dos partes. La primera establece que si una función es continua en un intervalo cerrado [a, b], entonces esta posee una integral definida en dicho intervalo. La segunda parte afirma que esta integral puede ser calculada utilizando una función primitiva.

Este teorema no solo simplifica el cálculo de áreas bajo curvas, sino que también proporciona una herramienta poderosa para abordar problemas en física, ingeniería y otras disciplinas. La comprensión de este teorema es esencial para cualquier estudiante o profesional que desee aplicar el cálculo integral en contextos prácticos.

Tipos de Integrales

Existen diversos tipos de integrales que son fundamentales para el estudio del cálculo integral. Las más comunes incluyen:

• Integrales Definidas: Estas integrales se utilizan para calcular el área bajo la curva de una función entre dos puntos específicos.
• Integrales Indefinidas: Estas representan una familia de funciones cuya derivada es la función original.
• Integrales Improprias: Utilizadas cuando los límites de integración son infinitos o cuando existe una discontinuidad en el intervalo.

Cada tipo de integral tiene sus propios métodos y técnicas de evaluación. Por ejemplo, las integrales definidas a menudo requieren el uso de sustituciones y propiedades específicas, mientras que las integrales impropias pueden requerir una evaluación límite para determinar su convergencia.

Aplicaciones del Cálculo Integral

Física y Ingeniería

Una de las aplicaciones más destacadas del cálculo integral se encuentra en el campo de la física. El cálculo integral es fundamental para el estudio de la cinemática, donde se utiliza para calcular la posición y la distancia recorrida por un objeto en movimiento. Además, se aplica en el análisis de fuerzas y trabajo, permitiendo determinar la energía realizada por una fuerza variable a lo largo de un trayecto.

En ingeniería, el cálculo integral también es esencial. Se utiliza para el diseño de estructuras, el análisis de sistemas de control, así como en la optimización de recursos. Por ejemplo, al calcular el centro de masa de un objeto, se requieren integrales para determinar la distribución de masa en diferentes secciones.

Economía y Estadística

El cálculo integral tiene aplicaciones significativas en economía y estadística. En economía, las integrales se utilizan para modelar y calcular costos totales y beneficios en relación con la producción. Este análisis permite a los economistas realizar proyecciones y evaluar la viabilidad de proyectos o políticas.

Por otro lado, en estadística, las integrales se emplean en la derivación de distribuciones de probabilidad, como la distribución normal. A través de la integración, se pueden calcular probabilidades y expectativas, lo cual es vital para la toma de decisiones basadas en datos.

Técnicas de Integración

Métodos Comunes de Integración

El cálculo integral incluye diversas técnicas que permiten resolver integrales complejas. Algunos de los métodos más utilizados son:

• Integración por Sustitución: Una técnica que transforma una integral difícil en una más fácil mediante un cambio de variable.
• Integración por Partes: Basada en la regla del producto de la derivación, esta técnica ayuda a resolver integrales de productos de funciones.
• Fracciones Parciales: Utilizada para integrar funciones racionales separándolas en elementos más simples.

Cada uno de estos métodos tiene sus propias aplicaciones y es esencial elegir la técnica adecuada para simplificar el proceso de integración. Dominar estas habilidades es crucial para estudiantes de matemáticas e ingenierías.

Herramientas Computacionales para la Integración

Con el avance de la tecnología, hoy en día existen herramientas computacionales que facilitan el cálculo integral. Software como MATLAB, Mathematica y Python ofrecen funcionalidades avanzadas para realizar integraciones, incluso para aquellas que no se pueden resolver analíticamente.

Estas herramientas permiten a los investigadores y profesionales realizar cálculos complejos en cuestión de segundos, lo que acelera el proceso de análisis y toma de decisiones. Además, su uso se ha vuelto indispensable en campos como la ingeniería, la física y la investigación científica, donde el tiempo y la precisión son críticos.

Preguntas Frecuentes

¿Cuál es el concepto básico del cálculo integral y cómo se diferencia del cálculo diferencial?

El cálculo integral se centra en la acumulación de cantidades y el cálculo de áreas bajo curvas, utilizando el concepto de integrales. Por otro lado, el cálculo diferencial se ocupa de las tasas de cambio y la pendiente de curvas a través de derivadas. La principal diferencia radica en que el cálculo integral se enfoca en sumar infinitas pequeñas partes para obtener un total, mientras que el cálculo diferencial se concentra en analizar cómo cambian las funciones.

¿Cuáles son las aplicaciones prácticas del cálculo integral en diferentes campos como la física y la economía?

El cálculo integral tiene diversas aplicaciones prácticas en varios campos:

1. Física: Se utiliza para calcular áreas bajo curvas, lo que permite determinar trabajo realizado por una fuerza variable y para encontrar volúmenes de cuerpos tridimensionales mediante la integración de funciones.

2. Economía: En este ámbito, el cálculo integral se aplica para evaluar costos totales a partir de funciones de costo marginal y para analizar ingresos totales mediante la integración de funciones de demanda.

Estas aplicaciones demuestran cómo el cálculo integral es fundamental para modelar y resolver problemas en distintas disciplinas.

¿Qué métodos existen para resolver integrales y en qué situaciones se utilizan cada uno?

Existen varios métodos para resolver integrales, cada uno adecuado para diferentes tipos de funciones:

1. Integración por sustitución: Se utiliza cuando una función puede ser transformada en una forma más simple mediante un cambio de variable.

2. Integración por partes: Eficaz para integrales que son el producto de dos funciones, aplicando la fórmula de integración por partes.

3. Integrales definidas e indefinidas: Las integrales indefinidas buscan una función primitiva, mientras que las definidas calculan el área bajo la curva entre dos límites.

4. Métodos numéricos: Se emplean cuando no se puede encontrar una solución analítica, utilizando aproximaciones como el método del trapecio o Simpson.

5. Integración de fracciones parciales: Útil para funciones racionales, descomponiendo la fracción en partes más simples.

Cada método se aplica en función de la naturaleza y complejidad de la integral a resolver.

¿Cómo se relaciona el Teorema Fundamental del Cálculo con el concepto de integral definida?

El Teorema Fundamental del Cálculo establece una conexión clave entre la diferenciación y la integración. Este teorema afirma que si una función es continua en un intervalo y se define su integral definida, entonces la derivada de la función primitiva (o antiderivada) es igual a la función original. Esto significa que calcular la integral definida de una función sobre un intervalo puede resolverse mediante su función primitiva, facilitando así el proceso de cálculo de áreas bajo la curva.

En conclusión, el cálculo integral no solo es fundamental en las matemáticas, sino que también tiene aplicaciones prácticas en diversas disciplinas. Su comprensión permite abordar problemas complejos de manera efectiva. Te invitamos a compartir este contenido y seguir explorando más sobre conceptos esenciales en nuestra serie de artículos.