Concepto De Diferencial En Cálculo Integral: Definición Clave

El concepto de diferencial en el cálculo integral es fundamental para comprender cómo se relacionan las funciones y sus tasas de cambio. Este principio se basa en la idea de que al estudiar cómo varía una función en torno a un punto específico, podemos determinar su comportamiento en intervalos infinitesimales. A lo largo de este artículo, exploraremos no solo la definición precisa de diferencial, sino también su aplicación práctica en el desarrollo de la integral y su relevancia en diversas áreas de la ciencia y la ingeniería.

Entender el diferencial no es solo una cuestión teórica, sino que también permite abordar problemas complejos de manera más efectiva. A medida que profundicemos en este concepto, descubrirás cómo las herramientas del cálculo integral facilitan el análisis y la resolución de situaciones cotidianas y avanzadas en matemática aplicada. ¡Sigue leyendo para enriquecer tu conocimiento sobre esta poderosa herramienta matemática!

Entendiendo el Concepto de Diferencial en el Cálculo Integral: Definición y Aplicaciones Esenciales

El concepto de diferencial en el cálculo integral es fundamental para comprender cómo las variaciones de una función se relacionan con su comportamiento. En términos sencillos, una diferencial representa un cambio infinitesimal en la variable independiente de una función. A continuación, se ofrecerá una definición más amplia y sus aplicaciones esenciales.

Definición de Diferencial

En el contexto del cálculo, la diferencial de una función ( f(x) ) se denota comúnmente por ( df ) y se define como:

[
df = f'(x) cdot dx
]

donde ( f'(x) ) es la derivada de la función y ( dx ) es un cambio infinitesimal en ( x ). Esta relación indica que el cambio en la función ( f ) (es decir, ( df )) se puede aproximar mediante el producto de la derivada de la función y un pequeño cambio en ( x ).

Aplicaciones Esenciales

Las diferenciales tienen diversas aplicaciones en el ámbito del cálculo integral, incluyendo:

• Estimación de Cambios: Las diferenciales permiten realizar estimaciones sobre el cambio en el valor de una función cuando ocurre un cambio pequeño en la variable independiente.
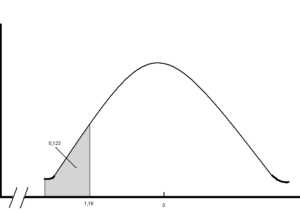
• Integral Definida: La integral definida se puede interpretar como la suma de infinitas diferenciales a lo largo de un intervalo. Esta interpretación es clave para entender el concepto de área bajo la curva.
• Cálculo de Error: En análisis numérico, las diferenciales son útiles para calcular errores de aproximación en métodos de integración.
• Transformaciones: En física e ingeniería, las diferenciales son fundamentales para cambiar variables en múltiples dimensiones y analizar el comportamiento de funciones complejas.

Propriedades de las Diferenciales

Las diferenciales poseen varias propiedades que son importantes en cálculos y aplicaciones matemáticas:

• Linealidad: Si ( y = af(x) + bg(x) ), entonces ( dy = a cdot df + b cdot dg ), donde ( a ) y ( b ) son constantes.
• Cadena de Derivadas: Si ( z = f(g(x)) ), entonces ( dz = f'(g(x)) cdot g'(x) cdot dx ).
• Regla del Producto: Si ( u = f(x) ) y ( v = g(x) ), entonces ( du cdot v + u cdot dv ) describe el cambio en el producto de dos funciones.

Conclusión de Aplicaciones

Las diferenciales son un componente esencial en el cálculo integral, proporcionando una base sólida para entender las variaciones en funciones y su correspondiente integración. Este enfoque no solo facilita la resolución de problemas matemáticos, sino que también tiene aplicaciones prácticas en campos como la física, la economía y la ingeniería. Al estudiar las diferenciales, se profundiza en el entendimiento del análisis matemático y se abre la puerta a conceptos más avanzados dentro del cálculo.

34 – Diferencial de una funcion. Concepto y Aplicacion CBC UBA

Curso de Integrales. Capítulo 2: la constante, el símbolo y el diferencial. Una propuesta didáctica.

¿Qué se entiende por diferencial en cálculo integral?

En el contexto de cálculo integral, el término diferencial se refiere a un concepto fundamental que ayuda a entender cómo se relacionan las funciones y sus cambios. Específicamente, el diferencial denota el cambio infinitesimal en una función y se usa para aproximar variaciones en situaciones donde los cambios son muy pequeños.

Cuando consideramos una función f(x), el diferencial de x, denotado como dx, representa un cambio infinitesimal en la variable independiente, mientras que el diferencial de la función, denotado como df, es el cambio correspondiente en la función f. Matemáticamente, se expresa como:

df = f'(x) dx

Aquí, f'(x) es la derivada de f, que indica la tasa de cambio de f con respecto a x. Este concepto de diferencial es crucial en el cálculo integral porque permite expresar el área bajo la curva de una función como la suma de muchos rectángulos infinitesimales, lo que se traduce en la integral definida.

En resumen, el diferencial es un concepto que facilita la conexión entre la derivación y la integración al permitirnos trabajar con cambios infinitesimales en el análisis de funciones.

¿Qué se entiende por diferenciación en el cálculo integral?

En el contexto del cálculo integral, la diferenciación se refiere al proceso mediante el cual se determina la tasa de cambio instantánea de una función respecto a una variable. En términos más formales, si tenemos una función ( f(x) ), su derivada ( f'(x) ) es el resultado de derivar ( f ) en relación a ( x ). Este proceso de diferenciación es fundamental porque permite entender cómo una función se comporta en diferentes puntos a lo largo de su dominio.

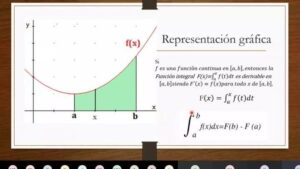
Por otro lado, la integración puede considerarse como el proceso inverso de la diferenciación. Mientras que la diferenciación busca encontrar la pendiente de la función en un punto específico, la integración se ocupa de calcular el área bajo la curva de dicha función en un intervalo determinado. Esta relación entre ambas operaciones se expresa en el Teorema Fundamental del Cálculo, que establece que:

1. Si ( F ) es una antiderivada de ( f ) en un intervalo ([a, b]), entonces:
[
int_a^b f(x) , dx = F(b) – F(a)
]

2. Esto implica que la integración y la diferenciación son procesos que se complementan entre sí, capace de transformar problemas de tasas de cambio en problemas de áreas.

En resumen, en el contexto del cálculo integral, la diferenciación es esencial para comprender la relación entre funciones, sus tasas de cambio y cómo estas se pueden revertir mediante la integración para calcular áreas y acumulaciones.

¿Qué se entiende por diferencial?

El término diferencial tiene varios significados según el contexto en el que se utilice, pero en general, se refiere a una diferencia o una variación entre dos o más elementos.

1. Matemáticas: En cálculo, el diferencial se refiere a un concepto que describe el cambio infinitesimal en una función. Se utiliza para establecer la pendiente de la tangente a la curva en un punto específico, y se simboliza comúnmente como dy o dx. El diferencial de una función se expresa como ( dy = f'(x) cdot dx ), donde ( f'(x) ) es la derivada de la función.

2. Economía: En este ámbito, el término se utiliza para referirse a la diferencia en precios o costos entre dos productos o servicios. Por ejemplo, el diferencial de tasas de interés se refiere a la diferencia entre las tasas de interés de dos préstamos o inversiones.

3. Física: En física, los diferenciales pueden referirse a cambios en magnitudes físicas, como el diferencial de energía o el diferencial de presión, que indican cómo varían estas magnitudes en relación con otros factores.

En resumen, el concepto de diferencial está relacionado con la idea de variación y cambio, y su aplicación puede ser muy diversa dependiendo del campo de estudio.

¿Qué significa un diferencial en integrales?

En el contexto de las integrales, un diferencial se refiere a un elemento infinitesimal que representa un cambio o una variación en una variable. Es un concepto fundamental en el cálculo y se utiliza para expresar el proceso de integración.

Cuando hablamos de una integral en forma definida, como:

[
int_a^b f(x) , dx
]

el diferencial (dx) indica que estamos considerando un pequeño cambio en la variable (x). Este (dx) es esencial porque permite sumar áreas infinitesimales bajo la curva de la función (f(x)) desde el punto (a) hasta el punto (b).

Más específicamente:

• El diferencial puede ser visto como el límite de la suma de una cantidad infinitamente pequeña, que se usa para calcular el área total bajo la curva.

• En términos de notación, cuando decimos (dx), nos referimos a la variable independiente que está siendo integrada.

• En el contexto de la integración, el diferencial también puede estar relacionado con el concepto de antiderivada, donde se busca una función cuya derivada nos dé la función original (f(x)).

En resumen, el diferencial en integrales es una representación crucial del cambio en la variable independiente, y su uso permite realizar el proceso de integración de manera precisa y efectiva.

Preguntas Frecuentes

En conclusión, el concepto de diferencial en cálculo integral es fundamental para comprender la relación entre la variación y el área bajo la curva. Este conocimiento no solo es esencial en matemáticas, sino también en diversas aplicaciones científicas. Te invitamos a compartir este contenido y a seguir explorando más sobre este fascinante tema.