La fuerza resultante es un concepto fundamental en la física que se refiere a la suma vectorial de todas las fuerzas que actúan sobre un cuerpo. Este valor determina el movimiento del objeto bajo la influencia de múltiples fuerzas, ya sean equilibradas o no. Comprender la fuerza resultante no solo es crucial para el estudio de la dinámica, sino que también tiene aplicaciones prácticas en diversas disciplinas como la ingeniería y la arquitectura.
A lo largo de este artículo, exploraremos en profundidad el significado de la fuerza resultante, cómo calcularla y su relevancia en situaciones cotidianas. Si deseas desentrañar los misterios de esta noción esencial y aprender a aplicarla en diferentes contextos, te invitamos a seguir leyendo.
Contenido
- 1 Entendiendo el Concepto de Fuerza Resultante: Definición y Aplicaciones en la Física
- 2 Fuerza Resultante Vertical con Trigonometría – Salvador FI
- 3 Como calcular la fuerza resultante con 3 cargas – Ley de Coulomb/Fuerza eléctrica
- 4 ¿Qué se entiende por fuerza resultante?
- 5 ¿Qué se entiende por fuerza resultante o neta?
- 6 ¿Cómo se puede representar la fuerza resultante?
- 7 ¿Qué se entiende por el vector fuerza resultante?
- 8 Preguntas Frecuentes
Entendiendo el Concepto de Fuerza Resultante: Definición y Aplicaciones en la Física
El concepto de fuerza resultante es fundamental en la física, ya que se refiere a la suma vectorial de todas las fuerzas que actúan sobre un objeto en particular. Esta fuerza resultante determina el comportamiento del cuerpo bajo la influencia de múltiples fuerzas, y es clave para entender el movimiento y la dinámica de los sistemas físicos.
Una fuerza se define como cualquier interacción que, al ser aplicada a un objeto, provoca un cambio en su estado de movimiento o en su forma. Estas fuerzas pueden ser clasificadas en diferentes tipos, como:
- Fuerzas de contacto: Actúan cuando dos objetos están en contacto directo. Ejemplos incluyen la fricción, la tensión y la normal.
- Fuerzas a distancia: Actúan sin necesidad de contacto físico. Ejemplos incluyen la gravedad, la electricidad y el magnetismo.
La fuerza resultante se obtiene al sumar todas las fuerzas que actúan sobre un objeto, teniendo en cuenta tanto la magnitud como la dirección de cada una de ellas. Matemáticamente, se expresa como:
Fuerza Resultante (FR) = F1 + F2 + F3 + … + Fn
donde cada Fi representa una fuerza individual actuando sobre el objeto. Este principio se basa en el principio de superposición, que establece que el efecto total de varias fuerzas sobre un objeto es igual a la suma de sus efectos individuales.
Para ilustrar la importancia de la fuerza resultante, es útil considerar algunas aplicaciones prácticas:
- Movimiento de vehículos: En el caso de un automóvil en movimiento, la fuerza resultante es crucial para entender cómo acelera, desacelera o cambia de dirección. Las fuerzas que actúan sobre el automóvil incluyen la fuerza del motor, la resistencia del aire, la fricción de los neumáticos y la gravedad.
- Equilibrio de estructuras: En ingeniería, se estudia la fuerza resultante para asegurar que las estructuras, como edificios y puentes, sean estables y seguras. La suma de las fuerzas debe ser cero para mantener el equilibrio estático.
- Dinamismo en deportes: En disciplinas deportivas, entender la fuerza resultante permite optimizar el rendimiento. Por ejemplo, en el lanzamiento de peso, la combinación de fuerzas aplicadas por el atleta determinará la distancia alcanzada.
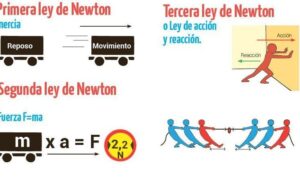
Es importante señalar que si la fuerza resultante es distinta de cero, el objeto experimentará una aceleración en la dirección de la fuerza resultante, de acuerdo con la segunda ley de Newton, que establece la relación entre fuerza, masa y aceleración:
Fuerza = Masa x Aceleración (F = ma)
Por el contrario, cuando la fuerza resultante es cero, el objeto permanecerá en su estado actual, sea en reposo o en movimiento uniforme, tal como lo dicta la primera ley de Newton o ley de inercia.
En resumen, el concepto de fuerza resultante es vital en la física para analizar situaciones dinámicas y estáticas, proporcionando un marco teórico sólido para entender cómo interactúan las fuerzas en el mundo real.
Fuerza Resultante Vertical con Trigonometría – Salvador FI
Como calcular la fuerza resultante con 3 cargas – Ley de Coulomb/Fuerza eléctrica
¿Qué se entiende por fuerza resultante?
La fuerza resultante se refiere a la suma vectorial de todas las fuerzas que actúan sobre un objeto. En otras palabras, es la fuerza única que puede sustituir a múltiples fuerzas individuales actuando en un cuerpo, manteniendo el mismo efecto sobre él.
En términos técnicos, cuando varias fuerzas se aplican simultáneamente a un objeto, estas pueden tener diferentes magnitudes y direcciones. Para obtener la fuerza resultante, se deben considerar tanto la magnitud como la dirección de cada una de las fuerzas involucradas.
El cálculo de la fuerza resultante es fundamental en la dinámica y la estática, ya que determina cómo se moverá o permanecerá en equilibrio el objeto bajo esas influencias. Si la fuerza resultante es cero, el objeto permanecerá en reposo o continuará con su movimiento uniforme; si no es cero, el objeto experimentará una aceleración en la dirección de la fuerza resultante, según lo establece la segunda ley de Newton.
En resumen, la fuerza resultante es crucial para comprender el comportamiento de los cuerpos en movimiento y en reposo, destacando así su relevancia en el estudio de la física.
¿Qué se entiende por fuerza resultante o neta?
En el contexto de la física, la fuerza resultante o fuerza neta se refiere a la suma vectorial de todas las fuerzas que actúan sobre un objeto. Esta fuerza se determina considerando tanto la magnitud como la dirección de cada fuerza aplicada.
Cuando múltiples fuerzas actúan sobre un mismo cuerpo, pueden ser aditivas o opuestas. La fuerza resultante es crucial para entender el movimiento del objeto, ya que determina su aceleración según la segunda ley de Newton, que establece que la fuerza neta es igual al producto de la masa del objeto y su aceleración (F = m * a).
Además, si la fuerza resultante es cero, el objeto permanece en su estado de reposo o movimiento uniforme, según el principio de inercia. En realidad, la fuerza resultante juega un papel fundamental en la disección de situaciones físicas y la resolución de problemas relacionados con el movimiento y la dinámica de los cuerpos.
¿Cómo se puede representar la fuerza resultante?
La fuerza resultante se puede representar como la suma vectorial de todas las fuerzas que actúan sobre un objeto. En este contexto, podemos definirla de la siguiente manera:
1. Vector de fuerza: Cada fuerza actuante se considera un vector, lo cual implica que tiene tanto una magnitud (cuánto) como una dirección (hacia dónde).
2. Suma de vectores: Para encontrar la fuerza resultante, se deben sumar todos los vectores de fuerza. Esto se puede hacer mediante métodos gráficos, como el polígono de fuerzas, o mediante cálculos matemáticos, utilizando las componentes de cada fuerza en los ejes cartesianos.
3. Fuerza resultante: La fuerza resultante se denota comúnmente como F_r y se calcula como:
F_r = F_1 + F_2 + … + F_n
donde F_1, F_2, …, F_n son las fuerzas individuales.
4. Representación gráfica: En un diagrama, la fuerza resultante se puede visualizar como la diagonal de un paralelogramo formado por dos fuerzas concurrentes, o como la línea que conecta el punto de inicio y el punto final de un conjunto de fuerzas.
5. Importancia: La fuerza resultante determina el movimiento del objeto, ya que según la segunda ley de Newton, un objeto acelerará en la dirección de la fuerza resultante aplicada.
En resumen, la fuerza resultante es crucial para entender cómo múltiples fuerzas interaccionan en un sistema y cómo afectan el movimiento de un objeto.
¿Qué se entiende por el vector fuerza resultante?
El vector fuerza resultante es un concepto fundamental en la física, específicamente en la mecánica. Se refiere a la suma vectorial de todas las fuerzas que actúan sobre un objeto. Cada fuerza tiene tanto una magnitud como una dirección, lo que las convierte en vectores.
Cuando múltiples fuerzas se aplican a un mismo objeto, estas pueden producir efectos combinados. El vector fuerza resultante proporciona una forma de representar este efecto neto. Para calcularlo, se deben considerar tanto las componentes en cada dirección (por ejemplo, las direcciones x e y en un sistema de coordenadas cartesianas) como las magnitudes y orientaciones de cada fuerza.
La importancia del vector fuerza resultante radica en que determina cómo se moverá el objeto en cuestión. Según la segunda ley de Newton, la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre él e inversamente proporcional a su masa. Esto se puede expresar con la fórmula:
F = m · a
donde F es la fuerza resultante, m es la masa del objeto y a es la aceleración. En resumen, el vector fuerza resultante es esencial para comprender y predecir el movimiento de los cuerpos bajo la acción de diversas fuerzas.
Preguntas Frecuentes
¿Qué es la fuerza resultante y cómo se calcula?
La fuerza resultante es la suma vectorial de todas las fuerzas que actúan sobre un objeto. Se calcula sumando cada fuerza en sus respectivas direcciones, teniendo en cuenta su magnitud y ángulo. Si las fuerzas están en la misma dirección, se suman directamente; si están en direcciones opuestas, se restan. En el caso de fuerzas en diferentes direcciones, se utilizan componentes para determinar la fuerza resultante mediante el teorema de Pitágoras y funciones trigonométricas.
¿Cuáles son las propiedades de la fuerza resultante en sistemas de fuerzas?
La fuerza resultante en sistemas de fuerzas tiene varias propiedades clave:
1. Vectorialidad: La fuerza resultante es un vector, lo que significa que tiene tanto magnitud como dirección.
2. Sumatoria: Se obtiene al sumar algebraicamente todas las fuerzas que actúan sobre un objeto, teniendo en cuenta sus direcciones.
3. Equilibrio: Si la fuerza resultante es cero, el sistema se encuentra en equilibrio, es decir, no hay cambio en el movimiento del objeto.
4. Movimiento: Si la fuerza resultante no es cero, provoca una aceleración en el objeto, según la segunda ley de Newton (F=ma).
Estas propiedades son esenciales para entender el comportamiento de los cuerpos bajo la acción de fuerzas.
¿Cómo afecta la fuerza resultante al movimiento de un objeto?
La fuerza resultante es la suma vectorial de todas las fuerzas que actúan sobre un objeto. Esta fuerza determina el movimiento del objeto, ya que si la fuerza resultante es diferente de cero, el objeto experimentará una aceleración en la dirección de la fuerza neta. Si la fuerza resultante es cero, el objeto mantendrá su estado de reposo o movimiento uniforme.
¿Qué papel juega la dirección en la determinación de la fuerza resultante?
La dirección es crucial en la determinación de la fuerza resultante porque afecta cómo se combinan las fuerzas individuales. Para calcular la fuerza resultante, es necesario considerar tanto la magnitud como la dirección de cada fuerza. Las fuerzas que actúan en la misma dirección se suman, mientras que las que actúan en direcciones opuestas se restan. Así, la dirección influye directamente en el sentido y la intensidad de la fuerza neta que se produce.
En conclusión, la fuerza resultante es fundamental para comprender los efectos de múltiples fuerzas en un sistema. Su análisis permite predecir el comportamiento de los cuerpos en movimiento. Te invitamos a compartir este contenido y a seguir explorando más conceptos esenciales en nuestra sección de definiciones.