El concepto de fuerza es fundamental en la física, ya que se define como cualquier interacción que, al ser ejercida, produce un cambio en el estado de movimiento de un cuerpo. Este principio se amplía al considerar la descomposición de fuerzas, un proceso que permite analizar las componentes de una fuerza en diferentes dimensiones. Este artículo se centrará en explicar la descomposición de fuerzas en 2 y 3 dimensiones, herramientas esenciales para resolver problemas en mecánica.
La capacidad de descomponer una fuerza en sus vectores constitutivos es crucial para entender fenómenos físicos complejos y facilitar cálculos en diversas aplicaciones de la ingeniería y la física. A lo largo de este texto, exploraremos los métodos y principios clave asociados a estas descomposiciones. Te invitamos a continuar leyendo para profundizar en estas importantes nociones.
Contenido
- 1 Comprendiendo el Concepto de Fuerza: Definición y Descomposición en Dos y Tres Dimensiones
- 2 PROBLEMA DE ECUACIONES CUADRÁTICAS. Corrección a @danielcarreon
- 3 Ley de Coulomb – Fuerza Resultante entre Cargas Eléctricas
- 4 Aplicaciones de la Fuerza en la Vida Cotidiana
- 5 Descomposición de Fuerzas en Dos Dimensiones
- 6 Descomposición de Fuerzas en Tres Dimensiones
- 7 Importancia de la Fuerza en el Estudio de la Física
- 8 Preguntas Frecuentes
Comprendiendo el Concepto de Fuerza: Definición y Descomposición en Dos y Tres Dimensiones
El concepto de fuerza es fundamental en la física y se define como cualquier interacción que, al ser aplicada a un cuerpo, provoca un cambio en su estado de movimiento o forma. En términos más técnicos, la fuerza se entiende como una magnitud vectorial que tiene tanto módulo como dirección y sentido.
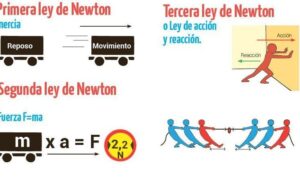
La expresión matemática de la fuerza se describe a través de la segunda ley de Newton, que establece que la fuerza neta (F) actuando sobre un objeto es igual al producto de su masa (m) y la aceleración (a) que experimenta, representada como:
F = m · a
Para un análisis más detallado, es esencial entender cómo se descompone la fuerza en diferentes dimensiones.
Descomposición de la Fuerza en Dos Dimensiones
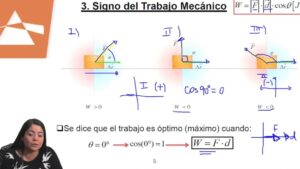
La descomposición de fuerzas en dos dimensiones es un proceso que permite expresar una fuerza resultante como la suma de sus componentes en un plano cartesiano, es decir, en las direcciones x e y. Para llevar a cabo esta descomposición, se suelen utilizar las funciones trigonométricas. Los pasos son los siguientes:
- Definir la fuerza resultante (F) y el ángulo (θ) respecto al eje x.
- Calcular la componente en x utilizando la fórmula: Fx = F · cos(θ).
- Calcular la componente en y usando la fórmula: Fy = F · sen(θ).
Este enfoque es fundamental en situaciones donde se requiere analizar fuerzas en un sistema bidimensional, como en el caso de un objeto en un plano inclinado.
Descomposición de la Fuerza en Tres Dimensiones
Cuando se trabaja en un espacio tridimensional, la descomposición de la fuerza se extiende a las tres dimensiones: x, y y z. Esto es esencial para tratar problemas más complejos en física e ingeniería. La descomposición se realiza de manera similar a la de dos dimensiones, pero incluye una tercera componente. Los pasos son:
- Identificar la fuerza resultante (F) y el ángulo (θ) con cada uno de los ejes.
- Calcular la componente en x: Fx = F · cos(θx).
- Calcular la componente en y: Fy = F · cos(θy).
- Calcular la componente en z: Fz = F · cos(θz).
Este método proporciona un marco integral para abordar problemas en contextos tridimensionales, como la dinámica en un entorno espacial.
La comprensión de la fuerza y su descomposición es crucial no solo en la física clásica, sino también en campos como la ingeniería estructural, la mecánica y la robótica. Cada situación puede requerir un análisis específico según la naturaleza de las fuerzas involucradas y los principios físicos que se aplican. Así, el dominio de este concepto permite a los científicos y a los ingenieros diseñar soluciones efectivas a problemáticas complejas en nuestro entorno físico.
PROBLEMA DE ECUACIONES CUADRÁTICAS. Corrección a @danielcarreon
Ley de Coulomb – Fuerza Resultante entre Cargas Eléctricas
Aplicaciones de la Fuerza en la Vida Cotidiana
Conceptos Básicos de Fuerza
La fuerza es una magnitud vectorial fundamental en la física, que se define como cualquier influencia capaz de modificar el estado de reposo o movimiento de un objeto. En la vida cotidiana, esta se manifiesta en diversas formas, desde empujar un carrito de supermercado hasta el rendimiento de vehículos en movimiento. Las fuerzas pueden clasificarse en diversas categorías, como fuerzas de contacto y fuerzas a distancia, donde cada tipo tiene su propio impacto en cómo los objetos interactúan entre sí.
Ejemplos Comunes de Fuerzas
En nuestra rutina diaria, encontramos múltiples ejemplos de fuerzas en acción. Por ejemplo, al levantar un objeto pesado, estamos aplicando una fuerza que contrarresta la gravedad. Asimismo, al frenar un automóvil, se genera una fuerza negativa que actúa sobre el movimiento del vehículo, deteniéndolo. Otros ejemplos incluyen la fricción, que permite que un coche no patine en una curva, y la tensión en una cuerda cuando se tira de ella.
- Fuerza gravitacional: Atrae objetos hacia el centro de la Tierra.
- Fuerza centrípeta: Mantiene un objeto en movimiento a lo largo de una trayectoria circular.
- Fuerza elástica: Se observa cuando se comprime o estira un resorte.
Descomposición de Fuerzas en Dos Dimensiones
Definición de Descomposición de Fuerzas
La descomposición de fuerzas es un proceso fundamental en la mecánica que permite dividir una fuerza en componentes más simples, facilitando así su análisis. En dos dimensiones, cualquier fuerza se puede descomponer en dos componentes ortogonales, generalmente en las direcciones horizontal y vertical. Esta técnica es crucial para resolver problemas complejos que involucran el movimiento de objetos.
Métodos de Descomposición de Fuerzas
Para llevar a cabo la descomposición de una fuerza en dos dimensiones, se utilizan técnicas de trigonometría. La fuerza se puede expresar en términos de sus componentes usando las funciones seno y coseno. Esto se representa generalmente con la siguiente fórmula:
- Fuerza en x (Fx) = F * cos(θ)
- Fuerza en y (Fy) = F * sin(θ)
Donde ( F ) es la magnitud de la fuerza original y ( θ ) es el ángulo formado con respecto al eje horizontal. Este proceso simplifica significativamente el análisis de sistemas en movimiento.
Descomposición de Fuerzas en Tres Dimensiones
Principios de Descomposición en 3D
La descomposición de fuerzas en tres dimensiones amplía la técnica utilizada en dos dimensiones, añadiendo una nueva componente a considerar, la dirección z. Este enfoque es vital en aplicaciones que requieren un análisis más completo de fuerzas que actúan en un espacio tridimensional, como en la ingeniería mecánica y en el diseño estructural.
Cálculo de Componentes en Tres Dimensiones
La descomposición de una fuerza en tres dimensiones se realiza utilizando fórmulas algebraicas análogas a las utilizadas en dos dimensiones. La magnitud de la fuerza se descompone en tres componentes, que se representan como sigue:
- Fuerza en x (Fx) = F * cos(θ) * cos(φ)
- Fuerza en y (Fy) = F * cos(θ) * sin(φ)
- Fuerza en z (Fz) = F * sin(θ)
Aquí, ( φ ) representa el ángulo de proyección sobre el plano xy, mientras que ( θ ) es el ángulo que forma la fuerza con el eje z. Este método permite una comprensión más precisa del comportamiento de los objetos bajo la influencia de múltiples fuerzas simultáneamente.
Importancia de la Fuerza en el Estudio de la Física
Fundamento de la Dinámica
La fuerza es un pilar esencial en el estudio de la dinámica, rama de la física que analiza el movimiento de los cuerpos. Comprender cómo las fuerzas afectan el movimiento permite predecir el comportamiento de los sistemas físicos de una manera precisa. El famoso principio de acción y reacción de Newton establece que para cada acción hay una reacción igual y opuesta, lo que resalta la importancia de las fuerzas en la interacción entre objetos.
Impacto en la Ingeniería y Tecnología
El análisis de fuerzas y su descomposición es igualmente crucial en diversos campos de la ingeniería y la tecnología. Ingenieros civiles, mecánicos y aeroespaciales utilizan estos principios para diseñar estructuras capaces de soportar cargas, así como para desarrollar sistemas de transporte eficientes. La comprensión profunda de cómo las fuerzas operan en diferentes dimensiones permite la creación de soluciones innovadoras y seguras en el diseño y la implementación de tecnologías avanzadas.
Preguntas Frecuentes
¿Qué es el concepto de fuerza en física y cómo se define?
El concepto de fuerza en física se refiere a una interacción que puede provocar un cambio en el estado de movimiento de un objeto. Se define como cualquier empuje o tirón que actúa sobre un cuerpo y se mide en newtons (N). En términos matemáticos, la fuerza se describe mediante la segunda ley de Newton, que establece que la fuerza es igual a la masa del objeto multiplicada por su aceleración (F = m · a).
¿Cómo se realiza la descomposición de fuerzas en dos dimensiones?
La descomposición de fuerzas en dos dimensiones se realiza desglosando una fuerza en sus componentes vertical y horizontal. Esto se logra utilizando las funciones trigonométricas seno y coseno, donde la componente x se obtiene multiplicando la fuerza por el coseno del ángulo respecto al eje x, y la componente y se calcula multiplicando la fuerza por el seno del ángulo respecto al eje x. Así, la fuerza original se representa como la suma de estas dos componentes: F = Fx + Fy.
¿Cuáles son los pasos para descomponer fuerzas en tres dimensiones?
Para descomponer fuerzas en tres dimensiones, se deben seguir los siguientes pasos:
1. Identificar la fuerza y sus componentes en el sistema de coordenadas.
2. Elegir un sistema de coordenadas apropiado (generalmente cartesiano: X, Y, Z).
3. Calcular las componentes de la fuerza utilizando las proyecciones sobre los ejes:
– Fuerza en X: ( F_x = F cdot cos(theta_x) )
– Fuerza en Y: ( F_y = F cdot cos(theta_y) )
– Fuerza en Z: ( F_z = F cdot cos(theta_z) )
4. Sumar las componentes para obtener la fuerza resultante.
Estos pasos permiten analizar y comprender mejor las fuerzas en un entorno tridimensional.
¿Qué importancia tiene la descomposición de fuerzas en el análisis de problemas físicos?
La descomposición de fuerzas es fundamental en el análisis de problemas físicos porque permite simplificar la comprensión de situaciones complejas. Al dividir una fuerza en sus componentes, se facilita el cálculo de su efecto en diferentes direcciones. Esto es esencial para resolver problemas de equilibrio y movimiento, garantizando así un análisis más preciso y efectivo.
En conclusión, comprender el concepto de fuerza y su descomposición en 2 y 3 dimensiones es fundamental para el análisis de situaciones físicas complejas. Esta base teórica permite abordar problemas de manera eficaz. Te invitamos a compartir este contenido y seguir explorando más sobre conceptos esenciales en la física.