Concepto De Función En Cálculo Integral: Fundamentos Esenciales

En el ámbito del cálculo integral, el concepto de función es fundamental para entender cómo se relacionan diferentes variables y cómo se puede transformar un área bajo una curva en un valor numérico. Una función, en términos matemáticos, es una relación que asigna a cada elemento de un conjunto un único elemento de otro conjunto, lo que permite modelar fenómenos en diversas disciplinas.

A través de este artículo, exploraremos en profundidad el concepto de función dentro del contexto del cálculo integral, desglosando sus características, propiedades y aplicaciones prácticas. A medida que avancemos, descubriremos cómo esta herramienta matemática proporciona las bases para resolver problemas complejos. ¡Sigue leyendo para desentrañar el poder de la función en el cálculo integral!

Comprendiendo el Concepto de Función en el Cálculo Integral: Definición y Aplicaciones Esenciales

El concepto de función es fundamental en el ámbito del cálculo integral, una rama de las matemáticas que se ocupa de la acumulación de cantidades. En este contexto, una función puede ser entendida como una relación entre un conjunto de entradas (dominio) y un conjunto de salidas (codominio), donde cada entrada está asociada a una única salida.

Definición de Función: Una función ( f ) se define formalmente como un conjunto de pares ordenados ((x, f(x))) donde ( x ) pertenece al dominio y ( f(x) ) es el valor asociado en el codominio. Para el cálculo integral, es crucial que la función sea continua en el intervalo considerado, lo que garantiza que no haya saltos o discontinuidades que puedan complicar el proceso de integración.

Las funciones se pueden clasificar de diversas maneras, algunas de las cuales incluyen:

• Funciones Algebraicas: Son aquellas que se pueden expresar mediante polinomios.
• Funciones Trigonométricas: Incluyen senos, cosenos y tangentes, fundamentales para problemas relacionados con ángulos y ciclos.
• Funciones Exponenciales y Logarítmicas: Se utilizan frecuentemente en contextos de crecimiento y decaimiento.

En el cálculo integral, la función juega un papel esencial en el proceso de determinar el área bajo una curva en un intervalo específico. El uso del concepto de función permite aplicar el teorema fundamental del cálculo, que establece que la integración y la diferenciación son procesos inversos.

Aplicaciones Esenciales del Cálculo Integral:
1. Cálculo de Áreas: La integral definida de una función permite calcular áreas entre la gráfica de la función y el eje x.
2. Volúmenes de Sólidos de Revolución: Al rotar una figura alrededor de un eje, se puede usar la integral para encontrar el volumen del sólido generado.
3. Trabajo y Energía: En física, la integral se utiliza para calcular el trabajo realizado por una fuerza variable a lo largo de un desplazamiento.
4. Modelado de Crecimiento: La integración es clave para modelar fenómenos de acumulación, como el crecimiento poblacional o el interés compuesto.

Además, la comprensión de las propiedades de las funciones, como la continuidad, la derivabilidad y la integrabilidad, es indispensable para poder aplicar adecuadamente las técnicas de integración. Por lo tanto, se debe prestar especial atención a los siguientes aspectos:

• Continuidad: Asegura que la función no presente saltos dentro del intervalo de integración.
• Derivabilidad: Indica que la función tiene una pendiente bien definida en todos los puntos del intervalo.
• Integrabilidad: Es necesario para garantizar que la suma de áreas, representadas por las integrales, converja a un valor finito.

Estos conceptos son esenciales no solo en matemáticas puras, sino también en aplicaciones prácticas en campos como la física, la ingeniería y la economía, donde el cálculo integral se utiliza para resolver problemas que implican cambios continuos. La interacción entre funciones y el cálculo integral revela un profundo y complejo entramado que es vital para la comprensión de muchas disciplinas científicas.

Antiderivada e integral indefinida de una función

Clase #1 de Integrales: Inmediatas y Cambio de Variable

¿Qué es una función integral?

Una función integral es un concepto fundamental en el campo del cálculo, especialmente en el análisis matemático. Se refiere a una función que se obtiene a partir de la integración de otra función, conocida como la función integrable.

En términos más específicos, si tenemos una función f(x), la función integral de f se denota comúnmente como F(x), donde:

F(x) = ∫ f(t) dt

Esto significa que F(x) es la antiderivada de f(x), lo que implica que la derivada de F(x) con respecto a x es igual a f(x). Es decir:

F'(x) = f(x)

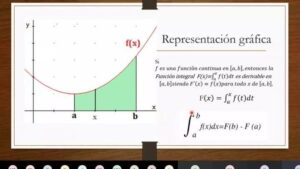
Una de las propiedades más importantes de las funciones integrales es el teorema fundamental del cálculo, que establece una conexión entre la diferenciación y la integración. Este teorema afirma que si una función f es continua en un intervalo [a, b], entonces:

∫(a to b) f(x) dx = F(b) – F(a)

Esto implica que el valor de la integral definida de f desde a hasta b puede calcularse utilizando la función integral F evaluada en los límites de integración.

En resumen, una función integral proporciona una manera de sumar infinitas contribuciones de una función en un intervalo, permitiendo así resolver problemas relacionados con áreas, volúmenes y otras aplicaciones en diversas ramas de la matemática y la física.

¿Qué es una función?

Una función es un concepto fundamental en matemáticas y otras disciplinas que describe una relación entre dos conjuntos. En términos simples, una función asigna a cada elemento de un conjunto (llamado *dominio*) exactamente un elemento de otro conjunto (llamado *codominio*).

Las características más importantes de una función son:

1. Dominio: El conjunto de todos los posibles valores de entrada.
2. Codominio: El conjunto de todos los posibles valores de salida.
3. Relación única: Cada elemento del dominio está relacionado con exactamente un elemento del codominio.

Matemáticamente, se puede denotar una función como ( f: A rightarrow B ), donde ( A ) es el dominio, ( B ) es el codominio y para cada ( x in A ), ( f(x) ) es el valor asociado en ( B ).

En resumen, una función es una herramienta que permite establecer relaciones y realizar operaciones a partir de ciertos valores, brindando una estructura y un orden a las matemáticas y a muchas otras áreas del conocimiento.

¿Qué es una función y puedes dar un ejemplo?

Una función es una relación matemática entre un conjunto de elementos, llamado dominio, y otro conjunto, llamado codominio, donde a cada elemento del dominio se le asigna exactamente un elemento del codominio. Esto significa que no puede haber dos salidas diferentes para el mismo valor de entrada.

En términos más simples, una función toma un valor de entrada (o variable independiente) y produce un único valor de salida (o variable dependiente). Las funciones son fundamentales en matemáticas y se utilizan en diversas disciplinas, desde la física hasta la economía.

Un ejemplo común de una función es la función cuadrática, que se expresa como:

f(x) = x²

En este caso, si tomamos un número del dominio, por ejemplo, 3, la función devuelve su cuadrado:

f(3) = 3² = 9

Aquí, 3 es el valor de entrada, y 9 es el valor de salida correspondiente. Lo importante es que cada valor de entrada tiene un único valor de salida, lo que caracteriza a una función.

¿Cómo se categorizan las funciones en cálculo integral?

En cálculo integral, las funciones se pueden categorizar de diversas maneras según diferentes criterios. A continuación, se presentan algunas de las categorías más relevantes:

1. Funciones Polinómicas: Estas son funciones de la forma ( f(x) = a_n x^n + a_{n-1} x^{n-1} + ldots + a_1 x + a_0 ), donde ( a_i ) son coeficientes y ( n ) es un entero no negativo. En este caso, la integral de una función polinómica se puede calcular utilizando la regla de potencias.

2. Funciones Racionales: Son aquellas que pueden expresarse como el cociente de dos polinomios, es decir, ( f(x) = frac{P(x)}{Q(x)} ), donde ( P(x) ) y ( Q(x) ) son polinomios. La integración de estas funciones a menudo requiere descomposición en fracciones parciales.

3. Funciones Trigonométricas: Estas incluyen funciones como ( sin(x) ), ( cos(x) ), ( tan(x) ), entre otras. La integración de funciones trigonométricas puede implicar identidades trigonométricas y técnicas específicas, como sustituciones trigonométricas.

4. Funciones Exponenciales y Logarítmicas: Las funciones de la forma ( f(x) = e^x ) (exponencial) o ( f(x) = ln(x) ) (logarítmica) tienen propiedades especiales que facilitan su integración. Por ejemplo, la integral de ( e^x ) es ( e^x + C ).

5. Funciones Hiperbólicas: Estas son análogas a las funciones trigonométricas, pero se basan en hipérbolas. Ejemplos comunes son ( sinh(x) ) y ( cosh(x) ). Sus integrales también se manejan con técnicas específicas.

6. Funciones Compuestas: Muchas veces, se integran funciones compuestas, que son combinaciones de las anteriores. En estos casos, se utilizan técnicas como la sustitución o integración por partes.

7. Funciones Definidas a Trozos: Estas son funciones que tienen diferentes expresiones en diferentes intervalos. Al integrar estas funciones, se debe considerar cada intervalo por separado.

Cada una de estas categorías tiene sus propias técnicas y métodos de integración, lo que permite abordar una amplia variedad de problemas en el cálculo integral. Es esencial entender estas clasificaciones para aplicar correctamente las estrategias de integración adecuadas en cada caso.

Preguntas Frecuentes

¿Qué es una función en el contexto del cálculo integral?

En el contexto del cálculo integral, una función es una relación matemática que asigna a cada número real de un conjunto (dominio) un único número real en otro conjunto (codominio). La integral de una función representa el área bajo la curva de esa función en un intervalo específico, permitiendo calcular acumulaciones, áreas y volúmenes.

¿Cómo se relaciona el concepto de función con el cálculo de áreas bajo la curva?

El concepto de función se relaciona con el cálculo de áreas bajo la curva a través de la integración. La integral definida de una función en un intervalo específico representa el área total entre la curva y el eje x. Así, al calcular esta integral, se obtiene la medida del área que corresponde a los valores de la función en ese intervalo.

¿Cuáles son las diferentes tipos de funciones que se utilizan en cálculos integrales?

En cálculos integrales, se utilizan diferentes tipos de funciones, entre las cuales destacan:

1. Funciones polinómicas: Son expresiones algebraicas que involucran potencias de una variable, como ( f(x) = ax^n + bx^{n-1} + … + c ).

2. Funciones trigonométricas: Incluyen senos, cosenos y tangentes, por ejemplo, ( f(x) = sin(x) ) o ( f(x) = cos(x) ).

3. Funciones exponenciales: Tienen la forma ( f(x) = a^x ), donde ( a ) es una constante positiva.

4. Funciones logarítmicas: Representadas como ( f(x) = log_a(x) ), son la inversa de las funciones exponenciales.

5. Funciones racionales: Estas son cocientes de funciones polinómicas, como ( f(x) = frac{p(x)}{q(x)} ).

Cada tipo de función tiene propiedades específicas que facilitan su integración y resolución dentro del cálculo integral.

¿Qué papel juegan las funciones continuas en el cálculo integral?

Las funciones continuas son fundamentales en el cálculo integral porque garantizan la existencia de la integral definida. Según el teorema fundamental del cálculo, si una función es continua en un intervalo cerrado, su integral puede calcularse y representa el área bajo la curva. Además, la continuidad asegura que no existan saltos o discontinuidades que dificulten la evaluación precisa de la integral.

En conclusión, el concepto de función en cálculo integral es fundamental para comprender diversas aplicaciones en matemáticas y ciencias. Su estudio permite una mejor comprensión de la variabilidad y el cambio. Te invitamos a compartir este contenido y seguir explorando más sobre estos conceptos esenciales para ampliar tu conocimiento.