Concepto De Función En Matemáticas: Definición Y Aplicaciones Básicas

En el vasto mundo de las matemáticas, el concepto de función se erige como uno de los pilares fundamentales que permiten entender diversas relaciones entre conjuntos. Una función es una correspondencia especial entre dos conjuntos, donde a cada elemento del primer conjunto le asignamos exactamente un elemento del segundo. Este concepto no solo es esencial en el ámbito académico, sino que también encuentra aplicaciones prácticas en campos como la economía, la física y la ingeniería.

A lo largo de este artículo, exploraremos en profundidad la definición de función, sus propiedades y tipos, así como su importancia en la resolución de problemas matemáticos. Acompáñanos en este recorrido para desentrañar el fascinante universo de las funciones y su relevancia en la comprensión de las matemáticas modernas.

Comprendiendo el Concepto de Función en Matemáticas: Definición, Tipos y Aplicaciones

El concepto de función en matemáticas es fundamental y se utiliza para representar relaciones entre conjuntos de números o variables. En términos simples, una función es una regla que asigna a cada elemento de un conjunto (llamado dominio) exactamente un elemento de otro conjunto (llamado codominio). Este concepto es crucial en diversas ramas de las matemáticas y otras ciencias.

Definición de función: Matemáticamente, una función se puede expresar como f: X → Y, donde X es el dominio y Y es el codominio. Para cada elemento x en X, hay un único elemento y en Y tal que f(x) = y. Es importante destacar que dos funciones son consideradas iguales si tienen los mismos dominios y asignan los mismos elementos en sus codominios.

Tipos de funciones: Existen diferentes tipos de funciones que se clasifican según diversas características. A continuación, se presenta una lista de algunos de los tipos más comunes:

• Funciones inyectivas: Una función es inyectiva si diferentes elementos del dominio tienen diferentes imágenes en el codominio. Es decir, si f(x1) = f(x2) implica que x1 = x2.
• Funciones sobreyectivas: Una función es sobreyectiva si cada elemento del codominio tiene al menos un elemento del dominio que se mapea a él. En otras palabras, la imagen de f cubre todo el codominio.
• Funciones biyectivas: Una función es biyectiva si es tanto inyectiva como sobreyectiva. Esto significa que existe una correspondencia uno a uno entre el dominio y el codominio.
• Funciones constantes: Son aquellas cuya imagen es siempre el mismo valor, independientemente del valor del dominio.
• Funciones polinómicas: Son funciones que se expresan como un polinomio de la forma f(x) = a_n * x^n + a_(n-1) * x^(n-1) + … + a_1 * x + a_0, donde a_i son coeficientes reales.

Aplicaciones de las funciones: Las funciones tienen múltiples aplicaciones en diferentes campos. Algunas de ellas incluyen:

• Matemáticas puras: Se utilizan para definir y estudiar relaciones matemáticas complejas.
• Física: Las funciones describen fenómenos físicos, como el movimiento, donde la posición puede ser una función del tiempo.
• Economía: En la economía, las funciones de oferta y demanda ayudan a modelar la relación entre precios y cantidades.
• Estadística: Las funciones de probabilidad son fundamentales para el análisis de datos y la toma de decisiones informadas.
• Informática: En programación, las funciones son bloques de código reutilizables que realizan tareas específicas.

Conclusión: Comprender el concepto de función y sus diversas clasificaciones y aplicaciones permite a los estudiantes y profesionales de distintas disciplinas abordar problemas complejos y expresar relaciones matemáticas efectivas.

CURSO DE FUNCIONES DESDE CERO. Lo más importante que tienes que saber

¿Qué es una Función? @MatematicasprofeAlex

¿Qué es una función en matemáticas?

En matemáticas, una función se define como una relación entre un conjunto de elementos llamado dominio y otro conjunto de elementos conocido como codominio. En esta relación, a cada elemento del dominio le corresponde exactamente un elemento del codominio. Esta propiedad asegura que no haya ambigüedad en la asignación de valores.

Formalmente, se puede expresar una función ( f ) como:

• ( f: A rightarrow B )

donde ( A ) es el conjunto de entrada (dominio) y ( B ) es el conjunto de salida (codominio). Si ( x ) es un elemento de ( A ), se denota como ( f(x) ) al resultado asociado en ( B ).

Ejemplos de funciones incluyen:

1. Función lineal: ( f(x) = mx + b ), donde ( m ) y ( b ) son constantes.
2. Función cuadrática: ( f(x) = ax^2 + bx + c ), donde ( a, b ) y ( c ) son constantes.

Las funciones pueden clasificarse según diferentes criterios, tales como:

• Inyectivas: Cuando diferentes elementos del dominio se asignan a diferentes elementos del codominio.

• Sobreyectivas: Cuando todos los elementos del codominio son alcanzados por al menos un elemento del dominio.

• Biyectivas: Cuando la función es tanto inyectiva como sobreyectiva.

En resumen, una función es una herramienta fundamental en matemáticas que permite establecer relaciones claras y precisas entre dos conjuntos de números u otros objetos.

¿Cómo se puede explicar la función?

La función es un concepto fundamental en matemáticas y en diversas áreas del conocimiento. Se puede definir como una relación entre dos conjuntos, donde a cada elemento del primer conjunto (denominado dominio) le corresponde exactamente un elemento del segundo conjunto (llamado codominio).

Componentes de una función:
1. Dominio: Es el conjunto de entrada de la función, donde se encuentran los valores que se pueden utilizar.
2. Codominio: Es el conjunto de salida, que incluye todos los posibles resultados de la función.
3. Regla de correspondencia: Es la relación o regla que establece cómo se vinculan los elementos del dominio con los del codominio.

Notación:
Las funciones se suelen denotar como ( f(x) ), donde ( f ) es el nombre de la función y ( x ) representa un elemento del dominio. El resultado de aplicar la función a ( x ) se escribe como ( f(x) ).

Tipos de funciones:

• Funciones lineales: Son aquellas que representan relaciones de tipo directo entre variables, donde el gráfico es una línea recta.

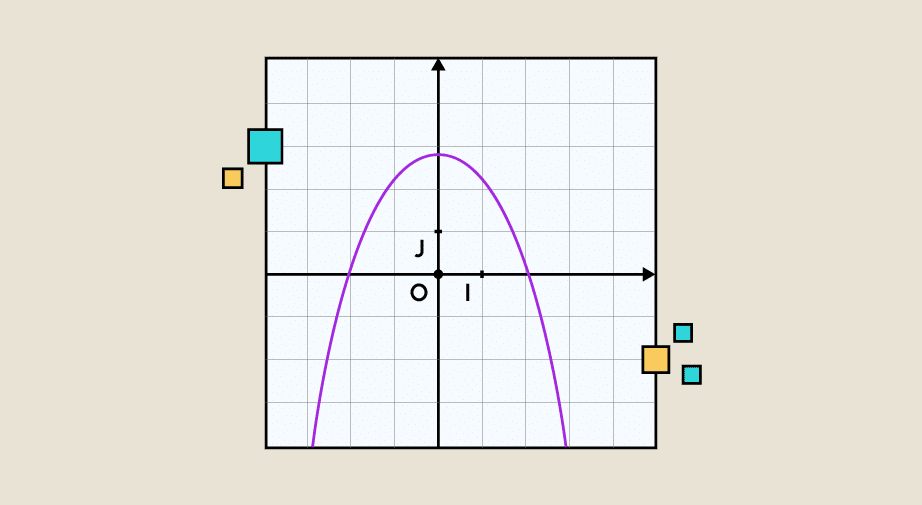
• Funciones cuadráticas: Son funciones polinómicas de segundo grado, cuyas gráficas son parábolas.

• Funciones exponenciales y logarítmicas: Representan crecimientos y decrecimientos en diferentes contextos.

Importancia de las funciones:
Las funciones son esenciales en matemáticas porque permiten modelar situaciones del mundo real y realizar análisis cuantitativos. Además, su estudio proporciona herramientas para resolver ecuaciones, optimizar problemas y entender fenómenos en diversas disciplinas como la física, la economía y la biología.

En resumen, la función es una herramienta clave en la matemática moderna que permite establecer conexiones entre distintas variables y facilitar la comprensión de relaciones complejas.

¿Cuál es la definición de una función?

En matemáticas, una función es una relación entre dos conjuntos que asigna a cada elemento del primer conjunto exactamente un elemento del segundo conjunto. Formalmente, se define como un par ordenado de conjuntos, donde el primer conjunto se denomina dominio y el segundo conjunto se denomina codominio.

Una función se puede representar de diversas maneras, como mediante una fórmula matemática, una tabla o un gráfico. Por ejemplo, si ( f ) es una función que toma un número ( x ) del dominio y lo transforma en ( y ) en el codominio, se puede escribir como ( y = f(x) ).

Es importante destacar que:

• Cada elemento del dominio tiene asociados uno y solo un elemento en el codominio.

• Si dos elementos del dominio diferentes pueden producir el mismo elemento en el codominio, la función sigue siendo válida.

En resumen, una función es una herramienta fundamental en matemáticas que permite modelar y analizar relaciones entre cantidades.

¿Qué significa función?

En el contexto de conceptos y definiciones, el término función se refiere a una relación o un vínculo entre dos o más elementos, donde a cada elemento de un conjunto le corresponde exactamente un elemento de otro conjunto. Es un concepto fundamental en diversas áreas del conocimiento, como las matemáticas, la informática y la biología.

En matemáticas, una función puede ser definida formalmente como un conjunto de pares ordenados ((x, y)) donde cada (x) pertenece a un conjunto llamado dominio y cada (y) a un conjunto conocido como codominio. Esto implica que para cada valor de (x) hay un único valor de (y) asociado.

En informática, el término también se utiliza para referirse a un bloque de código que realiza una tarea específica y puede ser invocado en diferentes partes de un programa, contribuyendo así a la organización y reutilización del código.

En resumen, el concepto de función implica una asociación clara y definida entre elementos, lo que permite entender y analizar relaciones en diversos contextos.

Preguntas Frecuentes

¿Qué es una función en matemáticas?

Una función en matemáticas es una relación entre un conjunto de entradas y un conjunto de salidas, donde a cada entrada le corresponde exactamente una salida. Se suele representar como f(x), donde x es el valor de entrada y f(x) es el valor de salida.

¿Cuáles son las principales características de una función?

Las principales características de una función son:

1. Dominio: Conjunto de valores de entrada (x) para los cuales la función está definida.
2. Rango: Conjunto de valores de salida (f(x)) que puede asumir la función.
3. Unicidad: Cada valor del dominio debe corresponder a un único valor en el rango; es decir, no puede haber dos salidas diferentes para el mismo valor de entrada.
4. Continuidad: En muchas funciones, los valores no presentan saltos o discontinuidades.

Estas características permiten conocer y analizar el comportamiento de las funciones matemáticas.

¿Cómo se representa gráficamente una función matemática?

Una función matemática se representa gráficamente trazando su gráfica en un sistema de coordenadas, donde el eje horizontal (Eje X) representa los valores de la variable independiente y el eje vertical (Eje Y) muestra los valores de la variable dependiente. Cada punto de la gráfica corresponde a un par ordenado (x, f(x)), donde f(x) es el resultado de la función para un valor dado de x.

¿Cuál es la diferencia entre una función inyectiva, sobreyectiva y biyectiva?

Una función se clasifica en tres tipos según su relación entre el conjunto de partida y el de llegada:

1. Inyectiva: Una función ( f: A to B ) es inyectiva si a elementos distintos de ( A ) les asigna elementos distintos de ( B ). Es decir, no hay dos elementos diferentes en ( A ) que se mapeen al mismo elemento en ( B ).

2. Sobreyectiva: Una función es sobreyectiva si cada elemento del conjunto ( B ) tiene al menos un elemento de ( A ) que se mapea a él. Esto significa que la imagen de ( f ) cubre todo el conjunto ( B ).

3. Biyectiva: Una función es biyectiva si es tanto inyectiva como sobreyectiva, lo que implica una correspondencia uno a uno entre los elementos de ( A ) y ( B ). Cada elemento de ( A ) se relaciona con un único elemento de ( B ) y viceversa.

En resumen:

• Inyectiva = no mapeo repetido,

• Sobreyectiva = cobertura total de ( B ),

• Biyectiva = correspondencia uno a uno.

  En conclusión, el concepto de función en matemáticas es fundamental para entender diversas relaciones y estructuras en este campo. Su estudio permite profundizar en el análisis y la resolución de problemas. Te invitamos a compartir este contenido y a seguir explorando más definiciones que enriquecerán tu conocimiento.