La función inversa es un concepto fundamental en matemáticas que nos permite deshacer el efecto de una función dada. En términos simples, si tenemos una función f(x) que transforma un valor x en otro valor y, la función inversa, denotada como f⁻¹(y), nos permite recuperar ese valor original x a partir de y. Este artículo explorará a fondo qué es una función inversa, cómo se determina y su importancia en diversas aplicaciones matemáticas. Si deseas comprender este concepto crucial y descubrir cómo se aplica en distintos contextos, ¡sigue leyendo!
Contenido
- 1 Entendiendo el Concepto de Función Inversa en Matemáticas: Definición y Aplicaciones
- 2 Función inyectiva, sobreyectiva y biyectiva | Tipos de funciones
- 3 Función Inversa – Cálculo de función inversa
- 4 ¿Cuál es el significado de función inversa en matemáticas?
- 5 ¿Qué se entiende por función inversa?
- 6 ¿Qué significa la función recíproca o inversa en matemáticas?
- 7 ¿Cuáles son ejemplos de la inversa?
- 8 Preguntas Frecuentes
Entendiendo el Concepto de Función Inversa en Matemáticas: Definición y Aplicaciones
La función inversa es un concepto fundamental en el ámbito de las matemáticas, que se refiere a la relación existente entre dos funciones. En términos simples, si tenemos una función ( f(x) ) que asigna un valor a cada entrada ( x ), la función inversa, denotada como ( f^{-1}(x) ), realiza la operación opuesta: toma el valor ( y ) (resultado de ( f(x) )) y devuelve el valor ( x ).
Para que una función tenga una inversa, debe ser bijectiva, lo que significa que debe ser tanto inyectiva (no puede asignar el mismo valor a diferentes entradas) como sobreyectiva (cubre todos los posibles valores de salida). Esta condición asegura que cada valor del dominio de ( f^{-1} ) corresponde a un único valor en el rango de ( f ) y viceversa.
La definición formal de la función inversa puede enunciarse de la siguiente manera:
- Si ( y = f(x) ), entonces ( x = f^{-1}(y) ).
Esto implica que aplicar la función ( f ) y luego su inversa ( f^{-1} ) devuelve el valor original, así como hacer lo contrario también tiene el mismo efecto:
- ( f(f^{-1}(y)) = y )
- ( f^{-1}(f(x)) = x )
Las aplicaciones de la función inversa son numerosas y se pueden encontrar en diversas áreas de las matemáticas, incluyendo, pero no limitado a:
- Resolución de ecuaciones: A menudo se utiliza para deshacer operaciones, permitiendo encontrar soluciones a ecuaciones.
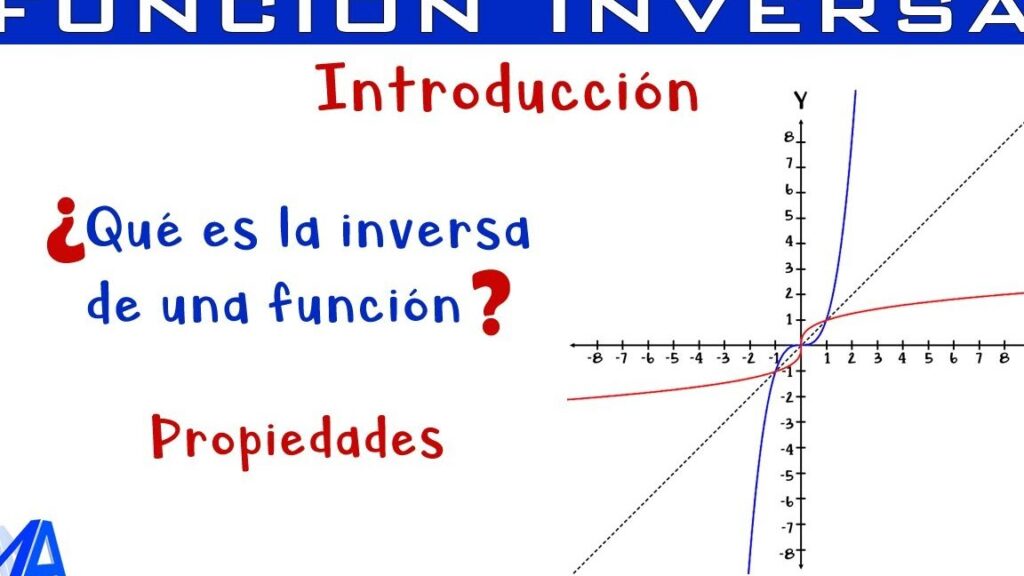
- Gráficas: La gráfica de una función inversa es simétrica respecto a la línea ( y = x ), lo cual facilita la visualización de relaciones entre variables.
- Teoremas de matemáticas avanzadas: Se encuentra en la demostración y aplicación de varios teoremas, como el Teorema de la Función Inversa en cálculo diferencial.
- Transformaciones: Las funciones inversas son útiles en transformaciones geométricas y en la manipulación de fórmulas en álgebra.
En resumen, la función inversa juega un papel crucial en múltiples contextos matemáticos. Su correcta comprensión permite a estudiantes y profesionales de las matemáticas manipular y resolver problemas complejos con mayor facilidad. Esta noción se extiende desde la resolución de ecuaciones hasta aplicaciones prácticas en diversas disciplinas científicas, donde el entendimiento de cómo deshacer operaciones resulta esencial para el desarrollo de teoría y métodos aplicados.
Función inyectiva, sobreyectiva y biyectiva | Tipos de funciones
Función Inversa – Cálculo de función inversa
¿Cuál es el significado de función inversa en matemáticas?
En matemáticas, una función inversa es una función que revierte el efecto de otra función. Si tenemos una función ( f(x) ), su función inversa se denota como ( f^{-1}(x) ). Esta relación significa que si aplicamos primero la función ( f ) a un número y luego aplicamos su inversa ( f^{-1} ), recuperamos el número original. En términos matemáticos, esto se expresa de la siguiente manera:
[
f(f^{-1}(x)) = x quad text{y} quad f^{-1}(f(x)) = x
]
Para que una función tenga inversa, debe ser bijectiva, es decir, ser tanto inyectiva (cada elemento del dominio se mapea a un único elemento del codominio) como sobreyectiva (cada elemento del codominio tiene al menos un elemento del dominio que se mapea a él).
En resumen, la función inversa permite deshacer la operación realizada por la función original, y es fundamental en diversas áreas de las matemáticas, como en la resolución de ecuaciones y en el estudio de relaciones funcionales.
¿Qué se entiende por función inversa?
En el contexto de conceptos y definiciones, una función inversa se refiere a una función que «deshace» los efectos de una función dada. Es decir, si tenemos una función f que convierte un número x en otro número y, entonces la función inversa de f, denotada como f-1, tomará y y lo convertirá nuevamente en x.
Formalmente, si f(x) = y, entonces para su función inversa se cumple que f-1(y) = x. Esto implica que las funciones inversas son una forma de revertir el proceso realizado por la función original.
Es importante señalar que no todas las funciones tienen inversas. Para que una función tenga una inversa, debe ser biyectiva, es decir, debe ser uno a uno (cada valor de x debe corresponder a un único valor de y) y sobreyectiva (cada valor posible de y debe ser alcanzable por algún valor de x).
En resumen, la función inversa permite encontrar el valor original a partir del resultado de aplicar una función, cumpliendo así una relación fundamental en matemáticas.
¿Qué significa la función recíproca o inversa en matemáticas?
La función recíproca o función inversa en matemáticas se refiere a una relación que «invierte» el efecto de otra función. Para entender mejor este concepto, es fundamental conocer algunas definiciones y propiedades.
1. Definición de función: Una función es una relación entre un conjunto de entrada (dominio) y un conjunto de salida (codominio) donde a cada elemento del dominio le corresponde exactamente un elemento del codominio.
2. Función inversa: La función inversa de una función ( f ), denotada generalmente como ( f^{-1} ), es aquella que permite recuperar el valor original del dominio a partir de un valor del codominio. En otras palabras, si ( y = f(x) ), entonces la función inversa satisface la relación ( x = f^{-1}(y) ).
3. Propiedades:
– Para que una función tenga una función inversa, debe ser biyectiva, es decir, debe ser inyectiva (cada elemento del codominio es imagen de a lo sumo un elemento del dominio) y sobreyectiva (cada elemento del codominio es imagen de al menos un elemento del dominio).
– Se cumple que ( f(f^{-1}(y)) = y ) y ( f^{-1}(f(x)) = x ).
4. Representación gráfica: En un gráfico, la función inversa se puede representar mediante una línea que es simétrica respecto a la línea ( y = x ). Esto significa que si un punto ( (a, b) ) pertenece a la gráfica de ( f ), entonces el punto ( (b, a) ) pertenecerá a la gráfica de ( f^{-1} ).
En resumen, la función recíproca o inversa es crucial para deshacer la acción de la función original, permitiendo así resolver ecuaciones y analizar relaciones entre variables de manera más efectiva.
¿Cuáles son ejemplos de la inversa?
En el contexto de conceptos y definiciones, la inversa se refiere a una relación o situación que es opuesta o contraria a otra. A continuación, se presentan algunos ejemplos de inversa en diferentes contextos:
1. Matemáticas: La inversa aditiva de un número es aquel número que, al sumarse, resulta en cero. Por ejemplo, la inversa aditiva de 5 es -5, ya que 5 + (-5) = 0.
2. Funciones: La inversa de una función es aquella que revierte el efecto de la función original. Si f(x) es una función, su inversa se denota como f⁻¹(x). Por ejemplo, si f(x) = 2x, la inversa sería f⁻¹(x) = x/2.
3. Lógica: En lógica proposicional, la inversa de una afirmación es el enunciado que niega tanto la hipótesis como la conclusión. Por ejemplo, si la afirmación es «Si llueve, entonces la calle está mojada», su inversa sería «Si no llueve, entonces la calle no está mojada».
4. Gramática: En el ámbito de la gramática, la inversa puede referirse a la inversión del orden de palabras en una oración. Por ejemplo, en lugar de «El perro ladra», se puede invertir a «Ladra el perro».
5. Relaciones Sociales: La inversa en relaciones puede referirse a un comportamiento opuesto. Por ejemplo, si alguien actúa con generosidad, su inversa sería actuar con egoísmo.
Estos ejemplos ilustran cómo el concepto de inversa se aplica en diversos contextos, mostrando la idea de oposición o reversibilidad.
Preguntas Frecuentes
¿Qué es una función inversa y cómo se determina a partir de una función dada?
Una función inversa es aquella que, al aplicarse a una función original, devuelve el valor inicial. Se determina a partir de una función dada ( f(x) ) intercambiando las variables ( x ) e ( y ) en la ecuación ( y = f(x) ) y resolviendo para ( y ). La función inversa se denota como ( f^{-1}(x) ). Para que una función tenga inversa, debe ser uno a uno, es decir, cada valor de ( y ) debe corresponder a un único valor de ( x ).
¿Cuáles son las propiedades fundamentales de las funciones inversas?
Las propiedades fundamentales de las funciones inversas son:
1. Inversibilidad: Una función tiene una función inversa solo si es bijectiva (inyectiva y sobreyectiva).
2. Composición: Si ( f ) es una función y ( f^{-1} ) es su inversa, se cumple que ( f(f^{-1}(x)) = x ) y ( f^{-1}(f(x)) = x ) para todo ( x ) en el dominio adecuado.
3. Simetría: El gráfico de la función inversa ( f^{-1} ) es la reflección del gráfico de ( f ) respecto a la línea ( y = x ).
Estas propiedades son clave para entender la relación entre funciones y sus inversas.
¿Cómo se grafica la función inversa de una función original?
Para graficar la función inversa de una función original, se puede seguir estos pasos:
1. Graficar la función original en un plano cartesiano.
2. Reflejar la gráfica de la función original respecto a la línea y = x, ya que la función inversa intercambia las coordenadas (x, y) de cada punto.
3. Asegurarse de que la función original sea bijectiva (es decir, que sea inyectiva y sobreyectiva) para que tenga una inversa válida.
Este proceso permite visualizar cómo la función inversa se relaciona con la función original.
¿En qué situaciones no existe una función inversa para una función dada?
Una función no tiene una función inversa cuando no es bijectiva, es decir, cuando no es inyectiva (no asigna valores únicos a cada elemento del dominio) o no es sobreyectiva (no abarca todo el codominio). Esto significa que si hay valores del codominio que no son alcanzados por la función o si un mismo valor del codominio es obtenido por diferentes elementos del dominio, la función carece de inversa.
En conclusión, el concepto de función inversa es fundamental en matemáticas, ya que permite deshacer operaciones y comprender relaciones entre variables. Profundizar en este tema enriquece nuestro conocimiento matemático. Te invitamos a compartir este contenido y a seguir explorando más conceptos esenciales en nuestras próximas publicaciones.