¿Te has preguntado alguna vez cómo se representan matemáticamente situaciones cotidianas? El concepto de función lineal es fundamental en el estudio de las matemáticas, ya que describe relaciones proporcionales entre dos variables. Una función lineal se define como aquella que puede expresarse en la forma y = mx + b, donde m es la pendiente y b es la intersección con el eje y.
A lo largo de este artículo, exploraremos en profundidad las características, propiedades y aplicaciones de las funciones lineales. Desde su representación gráfica hasta su uso en la resolución de problemas reales, comprender este concepto te permitirá desvelar un amplio espectro de fenómenos matemáticos y científicos. ¡Sigue leyendo para descubrir el fascinante mundo de las funciones lineales!
Contenido
- 1 Entendiendo el Concepto de Función Lineal en Matemáticas: Definición y Características Esenciales
- 2 Funciones Lineales de Primer Grado | Dominio, Rango, Pendiente Punto de Corte don los ejes y Gráfica
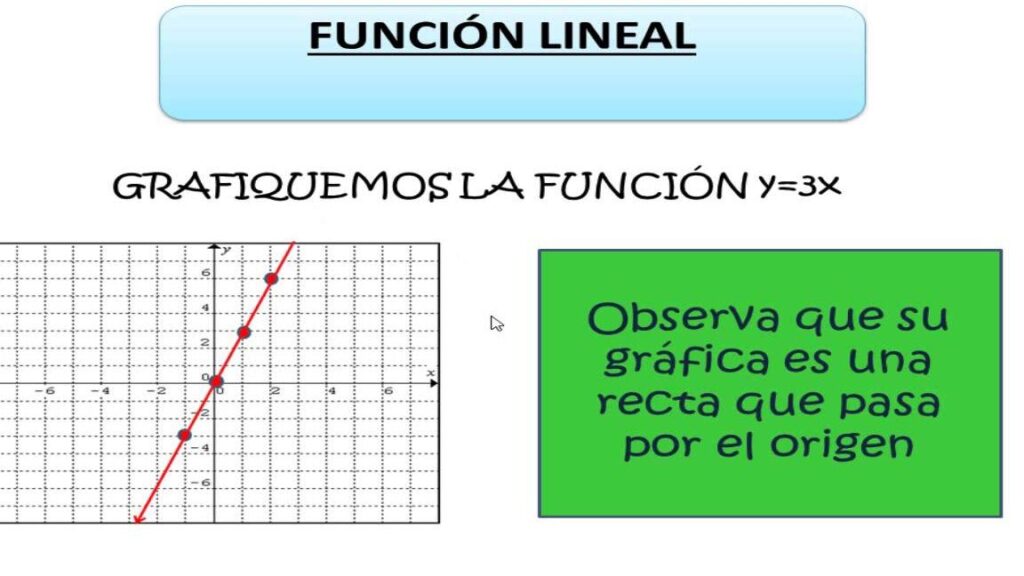
- 3 Gráfica de la función lineal | Ejemplo 1
- 4 ¿Qué es el concepto de una función lineal?
- 5 ¿Qué se entiende por una función lineal?
- 6 ¿Qué es una función lineal y cuáles son algunos ejemplos?
- 7 ¿Qué es una función lineal según Wikipedia?
- 8 Preguntas Frecuentes
Entendiendo el Concepto de Función Lineal en Matemáticas: Definición y Características Esenciales
El concepto de función lineal es fundamental en el ámbito de las matemáticas, ya que se utiliza para describir relaciones directas entre dos variables. Una función se considera lineal cuando su gráfica es una línea recta en el plano cartesiano. La forma general de una función lineal está dada por la ecuación:
y = mx + b
donde:
- m representa la pendiente de la recta, lo que indica la inclinación de la línea.
- b es el término independiente, que determina el punto donde la línea intersecta el eje y.
Las características esenciales de las funciones lineales son las siguientes:
- Monotonía: Las funciones lineales pueden ser crecientes o decrecientes, dependiendo del valor de la pendiente m. Si m > 0, la función es creciente; si m < 0, es decreciente.
- Dominio y rango: Tanto el dominio como el rango de una función lineal son todos los números reales (ℝ).
- Intersección: La función lineal siempre intercepta el eje y en el punto (0, b) y puede interceptar el eje x en el punto (-b/m, 0), siempre que m ≠ 0.
- Proporcionalidad: Si b = 0, la función se convierte en una función lineal que pasa por el origen, representando una relación directamente proporcional entre las variables.
Además, la pendiente es un aspecto crucial para entender el comportamiento de la función. La pendiente m indica qué tan rápido cambia la variable dependiente (y) en relación a la variable independiente (x). Por ejemplo, si m = 2, por cada unidad que se aumenta x, y aumenta en 2 unidades.
La representación gráfica de una función lineal es una línea recta, lo cual facilita la visualización de los valores y tendencias. En la práctica, las funciones lineales son ampliamente utilizadas en diversos campos, tales como la economía, la física y la ingeniería, debido a su capacidad para modelar situaciones del mundo real.
Existen algunos ejemplos comunes de funciones lineales:
- El cálculo de ingresos en función de las horas trabajadas, donde el ingreso es proporcional a las horas con un tarifa fija por hora.
- La relación entre temperatura en grados Celsius y Fahrenheit, que se puede expresar como una función lineal con una pendiente constante.
- El movimiento uniforme, donde la distancia recorrida es una función lineal del tiempo transcurrido.
En resumen, comprender el concepto de función lineal es vital para el desarrollo de habilidades matemáticas avanzadas. Este conocimiento no solo permite resolver problemas algebraicos, sino que también sienta las bases para el análisis y la interpretación de datos en contextos aplicados.
Funciones Lineales de Primer Grado | Dominio, Rango, Pendiente Punto de Corte don los ejes y Gráfica
Gráfica de la función lineal | Ejemplo 1
¿Qué es el concepto de una función lineal?
El concepto de una función lineal se refiere a un tipo de relación matemática que se puede representar mediante una ecuación de la forma y = mx + b, donde:
- y es la variable dependiente.
- x es la variable independiente.
- m es la pendiente de la recta, que indica la inclinación y la dirección de la función.
- b es el intersección con el eje y, es decir, el valor de y cuando x es igual a cero.
Las funciones lineales son caracterizadas por sus gráficas en forma de recta, lo que implica que su tasa de cambio (o pendiente) es constante. Esto significa que por cada incremento unitario en x, el cambio en y será siempre la misma cantidad multiplicada por m.
En resumen, una función lineal es una representación algebraica en la que hay una relación directa y proporcional entre las variables involucradas, lo que permite realizar predicciones y análisis económicos, físicos y de diversas disciplinas científicas.
¿Qué se entiende por una función lineal?
Una función lineal es un tipo de función matemática que se caracteriza por tener una relación directa y proporcional entre la variable independiente y la variable dependiente. Se puede expresar en la forma general:
f(x) = mx + b
donde:
- f(x) es el valor de la función para un determinado valor de x.
- m es la pendiente de la recta, que determina la inclinación y el sentido de la función (si es positiva o negativa).
- b es el término independiente, que representa el punto donde la recta cruza el eje Y.
Las gráficas de las funciones lineales son líneas rectas. La pendiente m indica cuánto cambia el valor de la función f(x) por cada unidad que se incrementa x. Si m es positiva, la función aumenta; si es negativa, la función disminuye.
En resumen, una función lineal es una relación matemática simple con un comportamiento constante, que se puede representar mediante una ecuación lineal y cuya gráfica es una línea recta en un sistema de coordenadas cartesianas.
¿Qué es una función lineal y cuáles son algunos ejemplos?
Una función lineal es una relación matemática que se representa mediante una ecuación de la forma y = mx + b, donde:
- y es la variable dependiente.
- x es la variable independiente.
- m es la pendiente de la recta, que indica el cambio en y por cada unidad que se cambia en x.
- b es el término constante, que representa el valor de y cuando x es igual a cero (el punto de intersección con el eje Y).
Las funciones lineales se grafican como líneas rectas en un plano cartesiano y tienen la propiedad de ser continuas y uniformemente cambiantes.
### Ejemplos de funciones lineales:
1. f(x) = 2x + 3: En esta función, la pendiente es 2 y la intersección con el eje Y es 3.
2. g(x) = -x + 4: Aquí, la pendiente es -1, lo que significa que por cada unidad que se aumenta en x, y disminuye en 1. La intersección con el eje Y es 4.
3. h(x) = 0.5x – 1: En este caso, la pendiente es 0.5, indicando un crecimiento gradual, y la intersección con el eje Y es -1.
En resumen, las funciones lineales son fundamentales en matemáticas y se utilizan en diversas aplicaciones, como en economía, física y ciencias sociales, para modelar relaciones proporcionales y constantes.
¿Qué es una función lineal según Wikipedia?
Una función lineal es un tipo de función matemática que se representa a través de una ecuación de la forma y = mx + b, donde:
- y es el valor de la variable dependiente.
- x es el valor de la variable independiente.
- m es la pendiente de la recta, que indica cómo cambia y en relación a x.
- b es el intercepto en el eje y, que representa el valor de y cuando x es igual a cero.
Las funciones lineales son importantes porque representan relaciones proporcionales y su gráfico es una línea recta en el plano cartesiano. Estas funciones son utilizadas en múltiples áreas como la economía, la física y la estadística para modelar situaciones donde hay una relación directa y constante entre dos variables.
En resumen, una función lineal es aquella que puede ser expresada como una recta y se caracteriza por tener una pendiente constante y un intercepto específico en el eje vertical.
Preguntas Frecuentes
¿Qué es una función lineal en matemáticas?
Una función lineal en matemáticas es una relación entre dos variables que se puede expresar en la forma y = mx + b, donde m es la pendiente y b es el valor de la intersección con el eje y. Esta función produce una gráfica lineal y representa una relación proporcional constante entre las variables.
¿Cuáles son las características principales de una función lineal?
Las características principales de una función lineal son:
1. Forma: Se expresa como y = mx + b, donde m es la pendiente y b es el punto de intersección con el eje Y.
2. Gráfica: Su representación gráfica es una recta.
3. Dominio y rango: Ambos son todos los números reales.
4. Proporcionalidad: Presenta una relación directamente proporcional entre las variables.
¿Cómo se representa gráficamente una función lineal?
Una función lineal se representa gráficamente como una línea recta en un plano cartesiano. Esta línea se puede definir mediante su ecuación general, que tiene la forma y = mx + b, donde m es la pendiente y b es la intersección con el eje y. La pendiente indica la inclinación de la línea, mientras que la intersección determina dónde cruza el eje y.
¿Cuál es la diferencia entre una función lineal y una función no lineal?
La diferencia entre una función lineal y una función no lineal radica en su representación gráfica y comportamiento. Una función lineal se expresa en la forma y = mx + b, donde su gráfico es una línea recta, representando una relación constante entre las variables. Por otro lado, una función no lineal no sigue esta regla y puede tener gráficos curvos, como parábolas o hipérbolas, indicando que la relación entre las variables varía de manera no uniforme.
En conclusión, el concepto de función lineal es fundamental en las matemáticas, ya que permite modelar relaciones directas entre variables. Comprender esta noción facilita el análisis y la resolución de problemas en diversas disciplinas. Te invitamos a compartir este contenido y a seguir explorando más definiciones y conceptos matemáticos en nuestro sitio.