El concepto de grado en matemáticas es fundamental para comprender diversas áreas de esta disciplina, especialmente en el contexto del álgebra y la teoría de polinomios. En términos simples, el grado de un polinomio se define como el exponente más alto de sus términos, lo que proporciona información crucial sobre su comportamiento y sus raíces. Este concepto no solo es esencial para resolver ecuaciones, sino que también juega un papel clave en la clasificación y análisis de funciones.
A medida que profundizamos en este artículo, exploraremos cómo el grado influye en la representación gráfica de las funciones, su aplicabilidad en problemas prácticos y las implicaciones que tiene en campos como la estadística y la física. Invito al lector a seguir leyendo para desentrañar los misterios y aplicaciones de este concepto tan vital en el ámbito matemático.
Contenido
- 1 Todo lo que necesitas saber sobre el concepto de grado en matemáticas: definición, significado y aplicaciones.
- 2 ¿QUÉ ES EL ÁLGEBRA? Super facil – Para principiantes
- 3 ECUACIONES DE PRIMER GRADO Super facil – Para principiantes
- 4 ¿Qué significa el término grado en matemáticas?
- 5 ¿Qué significa un grado?
- 6 ¿Qué significa el grado de una ecuación?
- 7 ¿Cuál es el grado de un término? ¿Puedes dar un ejemplo?
- 8 Preguntas Frecuentes
- 8.1 ¿Qué significa el término «grado» en el contexto de funciones matemáticas?
- 8.2 ¿Cómo se determina el grado de un polinomio?
- 8.3 ¿Cuál es la diferencia entre el grado de un polinomio y el grado de una ecuación algebraica?
- 8.4 ¿Por qué es importante conocer el grado de un polinomio en el análisis matemático?
Todo lo que necesitas saber sobre el concepto de grado en matemáticas: definición, significado y aplicaciones.
El concepto de grado en matemáticas es fundamental y se utiliza en diversas áreas del conocimiento. En términos generales, el grado puede tener múltiples significados dependiendo del contexto en que se aplique. A continuación, se presentan las principales definiciones y aplicaciones del grado en matemáticas.
Definición de grado
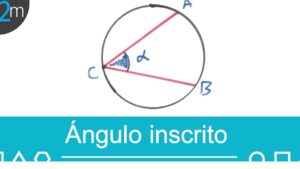
1. Grado en geometría: En este ámbito, el grado se refiere a la medida de un ángulo. Un círculo completo se divide en 360 grados, lo que permite expresar cualquier ángulo como un valor entre 0° y 360°. Esta medida es crucial para la resolución de problemas relacionados con triángulos, polígonos y otras figuras geométricas.
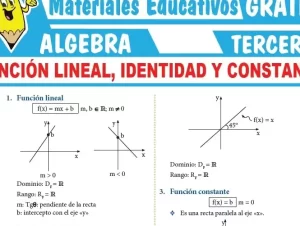
2. Grado de un polinomio: En el campo del álgebra, el grado de un polinomio se define como el mayor exponente de la variable en la expresión. Por ejemplo, el polinomio (3x^4 + 2x^3 – x + 7) tiene un grado de 4. Este concepto es esencial para entender el comportamiento de funciones polinómicas y su gráfica.
3. Grado en funciones: En el contexto de funciones racionales, el grado se refiere a la diferencia entre el grado del numerador y el grado del denominador. Este aspecto es vital para determinar asintotas verticales y horizontales al analizar el comportamiento de la función.
4. Grado de un vértice en grafos: En teoría de grafos, el grado de un vértice es la cantidad de aristas que inciden en él. Existen dos tipos de grado: el grado entrante (aristas que llegan al vértice) y el grado saliente (aristas que salen del vértice). Esta información es fundamental para el estudio de la conectividad y la estructura de los grafos.
Significado del grado
El grado, en cualquiera de sus aplicaciones, proporciona una forma cuantitativa de describir relaciones matemáticas. Su significado varía:
- En geometría, ayuda a establecer la medida de rotaciones y direcciones.
- En álgebra, permite clasificar polinomios según su complejidad.
- En análisis matemático, ayuda a comprender el comportamiento de funciones y sus características particulares.
- En teoría de grafos, permite evaluar la centralidad y la importancia de vértices dentro de una red.
Aplicaciones del grado
Las aplicaciones del concepto de grado son vastas y variadas:
- Ingeniería: En ingeniería civil, el grado se utiliza para calcular ángulos de inclinación en estructuras.
- Física: El grado es fundamental al medir dimensiones angulares en la mecánica clásica.
- Informática: En algoritmos de grafos, se utilizan los grados de los vértices para optimizar rutas y procesos de comunicación!
- Estadística: Al modelar relaciones entre variables mediante polinomios, se aplica el concepto de grado para identificar tendencias.
A través de estas definiciones y aplicaciones, se evidencia la relevancia del concepto de grado en diversos ámbitos del conocimiento matemático. Su comprensión adecuada es fundamental para la resolución de problemas y el desarrollo de teorías matemáticas avanzadas.
¿QUÉ ES EL ÁLGEBRA? Super facil – Para principiantes
ECUACIONES DE PRIMER GRADO Super facil – Para principiantes
¿Qué significa el término grado en matemáticas?
En matemáticas, el término grado puede tener diferentes significados dependiendo del contexto en el que se utilice. Aquí te presento dos de los más comunes:
1. Grado de un polinomio: El grado de un polinomio es el mayor exponente de la variable en la expresión algebraica. Por ejemplo, en el polinomio (3x^4 + 2x^3 – x + 5), el grado es 4, ya que el término con mayor exponente es (3x^4).
2. Grado de una función: En el contexto de funciones, el grado se refiere al grado del polinomio que representa a la función. Esto es especialmente relevante en el estudio de ecuaciones polinómicas y su comportamiento.
3. Grado de un vértice en un grafo: En teoría de grafos, el grado de un vértice es el número de aristas que inciden en él. Un vértice puede ser de grado alto o bajo, dependiendo de cuántas conexiones tenga.
Estos conceptos son fundamentales en diversas áreas de las matemáticas, incluyendo álgebra, cálculo y teoría de grafos.
¿Qué significa un grado?
En el contexto de conceptos y definiciones, un grado puede referirse a diferentes contextos dependiendo del área de estudio:
1. Geometría y Ángulos: Un grado es una unidad de medida utilizada para medir ángulos. Un círculo completo contiene 360 grados. Cada grado se divide en 60 minutos (min) y cada minuto en 60 segundos (s).
2. Temperatura: En la climatología y la física, un grado se utiliza para describir la temperatura. Las escalas más comunes son Celsius (°C) y Fahrenheit (°F), donde 0 °C corresponde al punto de congelación del agua y 100 °C al de ebullición.
3. Educación: En el ámbito académico, un grado se refiere a un nivel de educación o título obtenido, como un grado universitario (por ejemplo, licenciatura, maestría o doctorado).
4. Escalas de clasificación: En algunas disciplinas, un grado puede ser una forma de clasificar o medir la intensidad de un fenómeno, como en la escala de Richter para medir terremotos o la escala de Beaufort para medir vientos.
En resumen, el término grado es multifacético y su significado específico dependerá del contexto en el que se utilize.
¿Qué significa el grado de una ecuación?
El grado de una ecuación se refiere al exponente máximo de la variable en la ecuación. Este concepto es fundamental en el estudio de las ecuaciones algebraicas, ya que determina varias propiedades importantes de la ecuación y su comportamiento gráfico.
Por ejemplo, en una ecuación como ( ax^3 + bx^2 + cx + d = 0 ), el grado de la ecuación es 3, ya que el término con mayor exponente es ( x^3 ).
El grado también está relacionado con el número de soluciones que puede tener la ecuación. En general, una ecuación de grado ( n ) puede tener hasta ( n ) soluciones reales o complejas.
En resumen, el grado de una ecuación es un aspecto crucial que ayuda a clasificar y analizar las diferentes ecuaciones algebraicas.
¿Cuál es el grado de un término? ¿Puedes dar un ejemplo?
El grado de un término se refiere al número de variables que contiene un término algebraico. En otras palabras, indica el nivel o la potencia más alta de una variable dentro del término.
Por ejemplo, en el término 3x²y, el grado del término es 3, ya que suma las potencias de las variables: 2 (de x) + 1 (de y), lo que da como resultado 3.
En resumen, el grado de un término es importante para entender su comportamiento en ecuaciones y funciones algebraicas.
Preguntas Frecuentes
¿Qué significa el término «grado» en el contexto de funciones matemáticas?
El término grado en el contexto de funciones matemáticas se refiere al exponente más alto de la variable en un polinomio. Por ejemplo, en la función ( f(x) = 2x^3 + 3x^2 – x + 5 ), el grado es 3, ya que el exponente máximo es 3. Este valor indica la complejidad y el comportamiento de la función.
¿Cómo se determina el grado de un polinomio?
El grado de un polinomio se determina identificando el exponente más alto de la variable en sus términos. Por ejemplo, en el polinomio (3x^4 + 2x^3 – x + 5), el grado es 4 porque el término con el mayor exponente es (3x^4).
¿Cuál es la diferencia entre el grado de un polinomio y el grado de una ecuación algebraica?
La diferencia principal radica en su definición: el grado de un polinomio es el mayor exponente de sus variables, mientras que el grado de una ecuación algebraica se refiere al grado del polinomio que la compone. En resumen, el grado de un polinomio mide su complejidad, mientras que el grado de una ecuación indica la máxima potencia en su expresión algebraica.
¿Por qué es importante conocer el grado de un polinomio en el análisis matemático?
Conocer el grado de un polinomio es fundamental en el análisis matemático porque determina su comportamiento y propiedades. El grado indica el número máximo de soluciones que puede tener el polinomio y afecta la forma de su gráfica, así como su continuidad y diferenciabilidad. Además, el grado es clave para aplicar métodos de resolución y para entender la complejidad del polinomio en problemas de optimización y análisis de funciones.
En conclusión, el concepto de grado en matemáticas es fundamental para entender la naturaleza de las funciones y los polinomios. Su estudio permite una mejor comprensión de diversas áreas matemáticas. Te invitamos a compartir este contenido y a seguir explorando más conceptos relevantes en nuestro sitio. ¡La matemática te espera!