Concepto De Límite En Cálculo Integral: Entendiendo Su Importancia y Aplicaciones

El concepto de límite en cálculo integral es fundamental para entender cómo se relacionan las funciones con su comportamiento en puntos cercanos a valores específicos. Un límite se define como el valor al que se aproxima una función a medida que la variable independiente se acerca a un determinado punto. Este concepto no solo es crucial en el análisis matemático, sino que también sienta las bases para la comprensión de otras áreas del cálculo, como la continuidad y la derivación.

En este contexto, el límite permite establecer una conexión entre los valores infinitesimales y las integrales definidas, brindando herramientas esenciales para la resolución de problemas complejos. A lo largo de este artículo, exploraremos más a fondo cómo se aplica este concepto en el cálculo integral y su importancia dentro de la matemática. Te invitamos a continuar leyendo para profundizar en este tema fascinante y complejo.

Comprendiendo el Concepto de Límite en el Cálculo Integral: Definición y Aplicaciones Esenciales

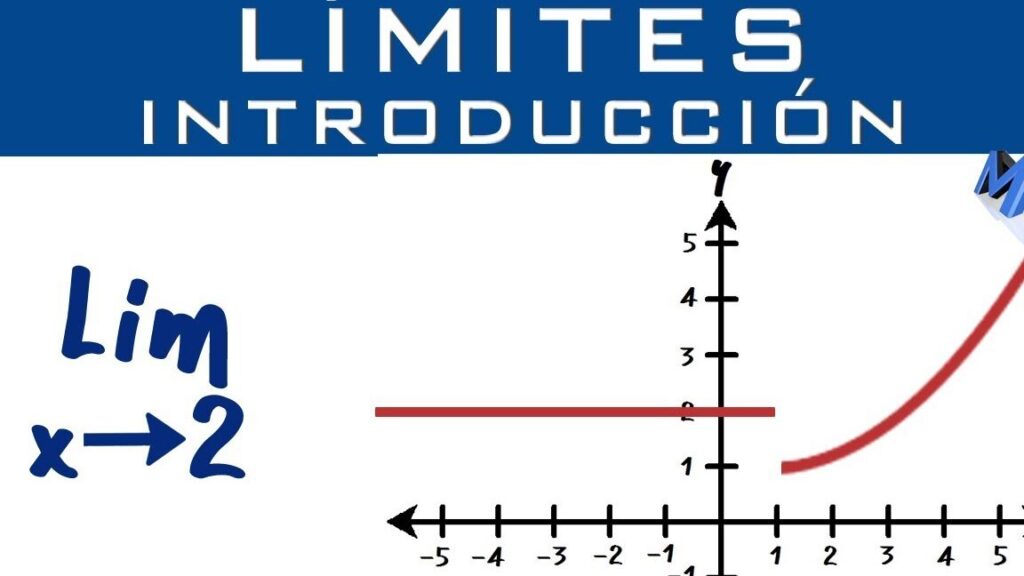
El concepto de límite es fundamental en el estudio del cálculo integral, ya que sienta las bases para la comprensión de muchas de sus propiedades y aplicaciones. Un límite se refiere al comportamiento de una función cuando la variable independiente se aproxima a un valor específico. Esto permite analizar y definir el cálculo de áreas bajo curvas y otros fenómenos matemáticos.

Definición de Límite: El límite de una función ( f(x) ) cuando ( x ) tiende a un valor ( a ) se denota como:

[
lim_{x to a} f(x) = L
]

donde ( L ) es el valor que ( f(x) ) se aproxima a medida que ( x ) se acerca a ( a ). En este contexto, es crucial distinguir entre límites finitos e infinitos, así como límites laterales, que son aquellos que se calculan considerando únicamente los valores que se acercan a ( a ) desde la izquierda o desde la derecha.

Aplicaciones Esenciales del Límite en el Cálculo Integral:

1. Definición de la Integral: La integral definida se basa en el concepto de límite. Se utiliza para calcular el área bajo la curva de la función ( f(x) ) entre dos puntos ( a ) y ( b ), utilizando el siguiente enfoque:

[
int_{a}^{b} f(x) , dx = lim_{n to infty} sum_{i=1}^{n} f(x_i^*) Delta x
]

donde ( Delta x ) representa el ancho de los subintervalos y ( x_i^* ) es un punto en cada subintervalo.

2. Teorema Fundamental del Cálculo: Este teorema establece la conexión entre derivación e integración. Se puede expresar como:

– Si ( F ) es una función antiderivada de ( f ) en el intervalo ([a, b]), entonces:

[
int_{a}^{b} f(x) , dx = F(b) – F(a)
]

Este resultado se fundamenta en la existencia de límites.

3. Continuidad y Límites: Para que una función sea integrable en un intervalo, debe ser continua casi en todas partes. El uso de límites ayuda a formalizar el concepto de continuidad y, por ende, garantizar la aplicabilidad de técnicas de integración.

• Proporciones en Análisis: Los límites permiten estudiar las tasas de cambio en los problemas de optimización.
• Análisis de Comportamiento Asintótico: A través de los límites, se pueden deducir comportamientos de funciones en el infinito, lo cual es esencial en el análisis de convergencia de series y secuencias.
• Resolución de Indeterminaciones: Los límites también son útiles para resolver formas indeterminadas en el cálculo de derivadas e integrales, utilizando métodos como la regla de L’Hôpital.

En resumen, el concepto de límite no solo es crucial para definir la integral, sino que también forma la base sobre la cual se construyen diversos teoremas y aplicaciones en el ámbito del cálculo integral.

Demostración Limite Usando Definición epsilon – delta. Ejemplo 1

Integrales definidas | Ejemplo 3

La importancia del límite en el cálculo integral

El concepto de límite es fundamental en el cálculo integral, ya que permite entender cómo se comportan las funciones a medida que se aproximan a un cierto valor. En este contexto, la noción de límite ayuda a establecer la base para la definición formal de la integral. La conexión entre límites e integrales se encuentra en la necesidad de calcular áreas bajo curvas y otras aplicaciones matemáticas.

Definición de límite y su relación con la continuidad

Para comprender la importancia del límite, es crucial definirlo. Un límite es el valor al que una función se aproxima a medida que su variable independiente se acerca a un punto específico. Esta definición está intrínsecamente relacionada con la continuidad de las funciones, lo que significa que no debe haber «saltos» o discontinuidades en el comportamiento de la misma alrededor del punto en cuestión.

• Cuando una función es continua, los límites existen y son iguales al valor de la función en ese punto.
• Las discontinuidades pueden causar problemas serios en el cálculo de integrales, ya que pueden alterar el área bajo la curva.

Por tanto, la continuidad es un requisito importante para la solvencia de muchos problemas en cálculo integral. Sin esta propiedad, los límites pueden no ser aplicables, lo que complica enormemente el análisis y las derivaciones posteriores.

Aplicaciones del límite en la teoría del cálculo

El cálculo de límites tiene varias aplicaciones en el ámbito de la matemática y la física. En particular, son fundamentales para la formulación de teoremas y propiedades que posteriormente se aplican en el cálculo integral. Por ejemplo, el Teorema Fundamental del Cálculo establece una conexión directa entre derivadas e integrales, y su demostración requiere un entendimiento sólido de límites.

Teorema de los límites y el cálculo integral

Uno de los principios más importantes del cálculo integral es el Teorema Fundamental del Cálculo. Este teorema establece que si una función es continua en un intervalo cerrado [a, b], entonces la integral definida de esta función en ese intervalo puede ser evaluada usando sus límites:

• La función primitiva F(x) es continua en [a, b].
• La integral definida se puede calcular como F(b) – F(a).

Este teorema no solo proporciona un método para calcular integrales, sino que también ilustra cómo los límites permiten la transición de una función a su integral asociada.

Ejemplos prácticos de límites en el cálculo integral

Los ejemplos concretos son esenciales para entender la aplicación de los límites en el cálculo integral. Estos ejemplos ayudan a visualizar cómo se relacionan los conceptos y cómo se aplican en diferentes contextos.

Ejemplo de cálculo de área bajo la curva

Uno de los ejemplos más comunes es calcular el área bajo la curva de una función f(x) en un intervalo [a, b]. Esto se logra a través de la suma de áreas de rectángulos (Riemann) que aproximan el área real. A medida que disminuimos el ancho de los rectángulos, se obtienen sumas Riemann que se convierten en el límite de la integral definida:

• Consideramos un número n de subdivisiones.
• Calculamos el área de cada rectángulo como f(ci) * Δx, donde ci es un punto en cada subintervalo.
• Tomamos el límite cuando n tiende a infinito.

Este proceso ilustra la interrelación entre límites e integrales: al calcular la suma de áreas a través del límite, obtenemos el valor exacto del área bajo la curva.

Desafíos comunes en el uso de límites en cálculo integral

A pesar de su utilidad, los límites presentan ciertos desafíos al aplicarlos en el contexto del cálculo integral. La comprensión de estos desafíos es esencial para evitar errores comunes.

Discontinuidades y límites indeterminados

Una dificultad significativa surge cuando la función presenta discontinuidades o se encuentra en situaciones que generan límites indeterminados. En estos casos, el límite puede no existir o ser difícil de calcular. Algunos problemas comunes incluyen:

• Funciones que tienen puntos de discontinuidad que afectan el cálculo del área.
• Casos en los que se necesita aplicar reglas como la regla de L’Hôpital para resolver límites indeterminados.

Es importante reconocer y manipular estas situaciones para obtener resultados apropiados en el contexto del cálculo integral.

Preguntas Frecuentes

¿Qué es el concepto de límite en cálculo integral y por qué es importante?

El concepto de límite en cálculo integral se refiere al valor al que se aproxima una función a medida que su variable independiente se acerca a un punto específico. Es fundamental porque permite definir de manera precisa el proceso de integración, que consiste en calcular áreas bajo curvas. Sin los límites, no podríamos establecer las bases del cálculo integral ni entender cómo sumar infinitas contribuciones de pequeñas áreas para obtener un total.

¿Cómo se aplica el concepto de límite en la definición de la integral?

El concepto de límite se aplica en la definición de la integral a través del proceso de aproximación de áreas bajo una curva. La integral se define como el límite de la suma de áreas de rectángulos (sumas de Riemann) cuando el número de rectángulos tiende a infinito y su ancho tiende a cero. Así, se establece que la integral definida es igual al límite de estas sumas en un intervalo dado.

¿Cuál es la relación entre el concepto de límite y la suma de Riemann?

La relación entre el concepto de límite y la suma de Riemann radica en que la suma de Riemann es un método para aproximar el área bajo una curva, y se basa en dividir el intervalo en subintervalos. A medida que el número de subintervalos aumenta y su ancho disminuye, la suma de Riemann converge a un valor que representa el integral definido de la función, el cual se define formalmente a través de límites. Por lo tanto, el límite permite formalizar la idea de convergencia en el cálculo del área bajo la curva.

¿Qué diferencia hay entre el límite en cálculo diferencial y el límite en cálculo integral?

En cálculo diferencial, el límite se utiliza para definir la derivada, que mide la tasa de cambio de una función en un punto específico. En cambio, en cálculo integral, el límite es fundamental para la definición de la integral, que calcula el área bajo una curva. Así, la principal diferencia radica en su uso: el límite en el contexto de derivadas y el límite en el contexto de áreas acumulativas.

En conclusión, el concepto de límite es fundamental en el cálculo integral, ya que permite entender la transición entre el cálculo diferencial y la integración. Este conocimiento es esencial para profundizar en temas avanzados de análisis matemático. Te invitamos a compartir este contenido y a seguir explorando nuestros artículos para expandir tu comprensión.