Concepto De Porcentaje En Matemáticas: Definición, Ejemplos y Aplicaciones

El concepto de porcentaje en matemáticas se refiere a una forma de expresar una cantidad como una fracción de 100. Se utiliza comúnmente para facilitar la comparación entre diferentes magnitudes, permitiendo así una interpretación más clara de datos numéricos en diversos contextos, desde la economía hasta la estadística. Un porcentaje se representa con el símbolo «%», y su cálculo implica una relación proporcional que puede ser de gran utilidad en la resolución de problemas.

Entender el porcentaje es fundamental para el análisis y la toma de decisiones informadas en situaciones cotidianas y profesionales. Este artículo abordará no solo la definición y los métodos de cálculo del porcentaje, sino también su aplicación práctica en diversas áreas. Te invitamos a continuar leyendo para profundizar en este importante concepto matemático.

Entendiendo el Porcentaje: Definición y Aplicaciones en Matemáticas

El porcentaje es una herramienta matemática fundamental que se utiliza para expresar una proporción en relación con un total. Se representa comúnmente utilizando el símbolo “%” y significa “por cada cien”. En términos más formales, un porcentaje indica cuántas partes de un total se consideran de un conjunto específico.

Definición de porcentaje: Un porcentaje se calcula dividiendo una cantidad específica por el total posible y multiplicando el resultado por 100. La fórmula puede expresarse de la siguiente manera:

Porcentaje (%) = (Parte / Total) × 100

Las aplicaciones del porcentaje son amplias y variadas, abarcando múltiples áreas del conocimiento. A continuación, se detallan algunas de las principales aplicaciones del porcentaje en matemáticas:

• Finanzas: Los porcentajes son esenciales para calcular intereses, ya sean simples o compuestos. Por ejemplo, al determinar el interés bancario, se utiliza un porcentaje sobre el capital inicial para calcular cuánto se ganará o pagará en un plazo determinado.
• Estadísticas: En la presentación de datos, los porcentajes permiten resumir información compleja de manera comprensible. Por ejemplo, las encuestas a menudo reportan resultados en porcentajes para facilitar la interpretación de apoyos o rechazos hacia un tema.
• Descuentos: En comercio, los porcentajes son cruciales para calcular rebajas y promociones. Un descuento del 20% sobre un producto que cuesta 50 euros significa que el consumidor pagará 40 euros.
• Proporciones en ciencias: En diversas disciplinas científicas, los porcentajes se usan para describir composiciones, como la concentración de soluciones químicas o la frecuencia de ciertos eventos en estudios biológicos.

Además de estas aplicaciones, el concepto de porcentaje también se manifiesta en situaciones cotidianas. Por ejemplo, al analizar resultados académicos, muchos estudiantes se ven familiarizados con sus calificaciones expresadas en formato de porcentaje, lo cual permite comparaciones directas entre diferentes evaluaciones o materias.

Algunas propiedades importantes de los porcentajes incluyen:

• Conversión: Es posible convertir un porcentaje en una fracción o decimal, facilitando así su utilización en cálculos matemáticos. Por ejemplo, un 25% puede expresarse como 1/4 o 0.25.
• Incrementos y decrecimientos: Los porcentajes permiten representar cambios porcentuales positivos o negativos. Esto es particularmente útil en análisis financieros o demográficos.
• Comparaciones: Los porcentajes facilitan la comparación entre diferentes cantidades, independientemente de su tamaño absoluto, permitiendo así una evaluación más equilibrada.

En resumen, el porcentaje es un concepto clave en matemáticas que permite simplificar la comprensión y representación de datos y relaciones numéricas, siendo una herramienta indispensable en diversas disciplinas académicas y en la vida cotidiana.

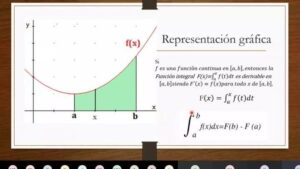
Representación gráfica de porcentajes: definición.

Cómo calcular el TANTO POR CIENTO % o porcentaje

Importancia del Porcentaje en la Vida Diaria

El concepto de porcentaje no solo es fundamental en el ámbito matemático, sino que también tiene una relevancia significativa en la vida cotidiana. Desde compras hasta ahorro y finanzas personales, los porcentajes son herramientas esenciales que nos permiten tomar decisiones informadas.

Aplicaciones Financieras

En el área de las finanzas, el porcentaje se utiliza para calcular diversos elementos, como intereses bancarios, impuestos y descuentos. Por ejemplo, cuando un banco ofrece un interés del 5% sobre una cuenta de ahorros, esto implica que cada año, el saldo crecerá en un 5%, lo cual es crucial para determinar el rendimiento de nuestras inversiones.

• Los préstamos suelen incluir tasas de interés expresadas en porcentaje.
• Los descuentos en tiendas frecuentemente se presentan como porcentajes reducidos sobre el precio original.
• Las tasas de inflación se comunican mediante porcentajes, afectando el poder adquisitivo de las personas.

Impacto en el Comercio

El uso de porcentajes en el comercio se manifiesta a través de descuentos y promociones. Las tiendas a menudo ofrecen precios reducidos, expresados como un porcentaje del precio inicial, lo que ayuda a atraer clientes y aumentar las ventas. Cuando un producto se vende con un 30% de descuento, esto no solo informa al consumidor sobre el ahorro, sino que también influye en su decisión de compra.

Porcentaje y Estadísticas

El porcentaje es una herramienta estadística que permite comparar datos de manera efectiva. En investigaciones, se utilizan porcentajes para expresar proporciones entre diferentes grupos o categorías, facilitando la comprensión de la información.

Interpretación de Datos

Cuando se presentan estudios o encuestas, los resultados suelen expresarse en forma de porcentaje, lo que permite una rápida visualización de tendencias. Por ejemplo, si se realiza una encuesta sobre la satisfacción del cliente y se determina que el 75% de los encuestados está satisfecho, esta cifra facilita la interpretación de la percepción general sobre el servicio ofrecido.

• Facilita comparaciones entre diferentes segmentos de la población.
• Permite evaluar el impacto de ciertas acciones o políticas.
• Ayuda a identificar áreas que requieren mejoras basadas en la proporción de respuestas negativas.

Representación Gráfica

Los gráficos de sectores y barras a menudo utilizan porcentajes para representar de manera visual las proporciones relativas. Esto no solo mejora la comprensión del público sobre los datos, sino que también destaca patrones de comportamiento, preferencias y resultados.

Errores Comunes al Calcular Porcentajes

A pesar de su simplicidad, el cálculo de porcentajes puede llevar a errores comunes que afectan la precisión de los resultados. Comprender estos errores es esencial para el correcto manejo del concepto.

Uso Incorrecto de la Fórmula

Un error frecuente ocurre al emplear incorrectamente la fórmula básica para calcular porcentajes. La fórmula correcta es:

Porcentaje = (Parte/Total) × 100

Si se confunden estos valores, se pueden obtener resultados completamente erróneos. Por ejemplo, si alguien intenta calcular el porcentaje de estudiantes aprobados en un examen sin tomar en cuenta el total de alumnos, el resultado será engañoso y no reflejará la realidad.

Confusión con Decimales

Otro error común radica en la conversión de decimales a porcentajes. Es fundamental recordar que un decimal debe multiplicarse por 100 para convertirse en porcentaje. Por ejemplo, un valor decimal de 0.25 se traduce en un 25%. La omisión de este paso puede dar lugar a interpretaciones incorrectas que afectan decisiones financieras o estadísticas.

Relación del Porcentaje con Otras Áreas Matemáticas

El porcentaje no se encuentra aislado dentro de las matemáticas, sino que tiene interrelaciones significativas con otros conceptos, como fracciones y decimales.

Conexión con Fracciones

El porcentaje se puede considerar como una fracción con un denominador de 100. Esta perspectiva permite entender mejor cómo se pueden transformar los porcentajes en fracciones y viceversa. Por ejemplo, un porcentaje del 40% es equivalente a la fracción 40/100, que se simplifica a 2/5.

Relación con Decimales

Del mismo modo, los porcentajes están relacionados con los números decimales. Para convertir un porcentaje en decimal, simplemente se debe dividir el porcentaje entre 100. Por ejemplo, un porcentaje del 85% se convierte en el decimal 0.85. Esta relación es especialmente útil en diversas aplicaciones matemáticas y financieras, donde se requiere trabajar con diferentes formatos numéricos.

Preguntas Frecuentes

¿Qué es un porcentaje y cómo se calcula en matemáticas?

Un porcentaje es una forma de expresar una cantidad como una fracción de 100. Se utiliza para comparar proporciones y entender relaciones entre números. Para calcular un porcentaje, se utiliza la siguiente fórmula:

(Parte / Total) × 100.

Por ejemplo, si tienes 20 de 200, el cálculo sería (20 / 200) × 100 = 10%.

¿Cuál es la diferencia entre porcentaje y fracción?

La diferencia entre porcentaje y fracción radica en su representación. Un porcentaje es una forma de expresar una cantidad como una parte de cien, utilizando el símbolo %. Por otro lado, una fracción representa una parte de un todo, expresada como el cociente de dos números, donde el número superior (numerador) indica cuántas partes se toman y el inferior (denominador) cuántas partes hay en total.

¿Cómo se aplica el concepto de porcentaje en situaciones cotidianas?

El concepto de porcentaje se aplica en diversas situaciones cotidianas, como por ejemplo en las rebajas de precios, donde se indica cuánto se reduce el valor de un producto. También es común en calculos de propinas, donde se calcula un porcentaje del total de la cuenta. Otro uso frecuente es en el ámbito de finanzas personales, para determinar el interés de ahorros o préstamos. En resumen, el porcentaje nos ayuda a comprender y manejar mejor las cantidades relativas en distintas situaciones.

¿Qué son los porcentajes equivalentes y cómo se encuentran?

Los porcentajes equivalentes son diferentes formas de representar la misma proporción o cantidad en relación a un total. Para encontrarlos, se pueden utilizar las siguientes fórmulas:

1. Conversión de fracciones a porcentajes: Multiplica la fracción por 100.
2. Conversión de decimales a porcentajes: Multiplica el número decimal por 100.

Por ejemplo, para convertir 0.75 a porcentaje, se realiza la operación (0.75 times 100 = 75%). Así, diferentes representaciones numéricas pueden ser comparadas o equivalentes al mismo porcentaje.

En conclusión, el porcentaje es un concepto fundamental en matemáticas que permite la comparación y análisis de datos en diversas aplicaciones. Comprender su definición y cálculo es esencial para el desarrollo de habilidades matemáticas. Te invitamos a compartir este contenido y a seguir explorando más conceptos clave en nuestras próximas publicaciones.