Concepto De Primer Miembro En Matemáticas: Definición y Ejemplos

El concepto de primer miembro en matemáticas se refiere a la primera parte de una ecuación o expresión que establece una relación entre diferentes elementos. Este término es fundamental para comprender el funcionamiento de las ecuaciones y sistemas numéricos, ya que permite desglosar y analizar las interacciones matemáticas. En este artículo, exploraremos no solo su definición precisa, sino también su importancia y aplicaciones en diversas áreas de la matemática.

A medida que profundizamos en este fascinante tema, descubriremos cómo el primer miembro juega un papel esencial en la resolución de problemas y la formulación de teoremas. Entender este concepto enriquecerá tu conocimiento matemático, facilitando la comprensión de estructuras más complejas. ¡Sigue leyendo para desentrañar todos los secretos del primer miembro!

Entendiendo el Concepto de Primer Miembro en Matemáticas: Definición y Aplicaciones

El término primer miembro es fundamental en matemáticas, especialmente en el ámbito de las ecuaciones y expresiones algebraicas. Este concepto se refiere al primer término de una relación de igualdad, específicamente en la forma estructurada de una ecuación matemática.

Definición de Primer Miembro

Un primer miembro es la expresión o conjunto de términos que precede al signo igual (=) en una ecuación. Se le atribuye un papel crucial porque establece la base para la resolución de la ecuación. En matemáticas, es común encontrar ecuaciones representadas de la siguiente manera:

• Primer Miembro: la parte izquierda de la ecuación.
• Segundo Miembro: la parte derecha de la ecuación.

Por ejemplo, en la ecuación ( 2x + 5 = 11 ), el primer miembro es ( 2x + 5 ) y el segundo miembro es ( 11 ).

Importancia en la Resolución de Ecuaciones

El primer miembro tiene varias aplicaciones fundamentales en el proceso de resolución de ecuaciones:

• Identificación de Incógnitas: Permite reconocer los términos que necesitan ser manipulados o despejados para encontrar el valor de la variable.
• Aplicación de Propiedades Algebraicas: En el primer miembro, se pueden aplicar diversas propiedades, como la propiedad distributiva o asociaciones, para simplificar expresiones.
• Establecimiento de Relación: Facilita la comparación entre las cantidades expresadas en el primer y segundo miembro, lo que es esencial para llegar a soluciones.

Ejemplos Prácticos

La comprensión del concepto de primer miembro es esencial en diversos contextos matemáticos. Aquí hay algunos ejemplos prácticos:

• En problemas de física donde se utilizan ecuaciones para describir fenómenos, el primer miembro puede representar fuerzas o energías que se equilibran.
• En matemáticas financieras, se emplea en la formulación de ecuaciones para calcular intereses, donde el primer miembro representa el capital inicial más los intereses acumulados.
• En geometría, se usa en ecuaciones que describen propiedades de figuras, donde el primer miembro puede reflejar parámetros como áreas o perímetros en relación con otras variables.

Desafíos Relacionados

Entender el primer miembro no solo implica saber su definición, sino también identificar los desafíos que surgen durante su uso. Estos incluyen:

• Análisis de Errores: La manipulación incorrecta del primer miembro puede llevar a errores en la solución.
• Confusión en Términos: Algunos estudiantes confunden el primer miembro con el segundo, lo que puede complicar la resolución.
• Soluciones Múltiples: En ciertas ecuaciones, el primer miembro puede generar resultados que requieren interpretación adicional para entender todas las posibles soluciones.

El concepto de primer miembro es, por tanto, crucial en diversas áreas de estudio dentro de las matemáticas. Su correcta comprensión y manejo son esenciales para resolver problemas matemáticos de manera efectiva.

Cómo solucionar una ecuación entera de primer grado | Ejemplo 1

Solución de problemas con Ecuaciones de Primer Grado | Ejemplo 1

¿Qué se entiende por un miembro de la ecuación?

En el contexto de las matemáticas, un miembro de la ecuación se refiere a cada una de las partes que componen una ecuación. Una ecuación es una relación matemática que establece la igualdad entre dos expresiones algebraicas, y está compuesta por dos miembros: el miembro izquierdo y el miembro derecho.

Por ejemplo, en la ecuación 2x + 3 = 7, el lado izquierdo (2x + 3) es el miembro izquierdo y el lado derecho (7) es el miembro derecho. Cada uno de estos miembros puede contener números, variables y operaciones matemáticas.

El objetivo al resolver una ecuación es encontrar el valor de las variables presentes para que ambos miembros sean iguales, manteniendo así la equivalencia establecida por la ecuación.

¿Qué es una ecuación de primer grado?

Una ecuación de primer grado es una expresión matemática que establece la igualdad entre dos cantidades, donde la variable (usualmente representada por (x)) tiene un exponente de uno. En otras palabras, es una ecuación que se puede escribir en la forma estándar:

ax + b = 0

donde:

• a y b son coeficientes numéricos,

• a no puede ser cero (si a fuera cero, la ecuación dejaría de ser de primer grado), y

• x es la variable que se desea resolver.

El objetivo principal al trabajar con una ecuación de primer grado es encontrar el valor de (x) que satisface la igualdad. Por lo general, este tipo de ecuaciones tiene una única solución, lo que significa que hay un único valor de (x) que cumple con la condición establecida por la ecuación.

Las ecuaciones de primer grado se utilizan en diversas aplicaciones en matemáticas, ciencias y economía, ya que proporcionan un modelo para situaciones lineales.

¿Qué implica que una función sea de primer grado?

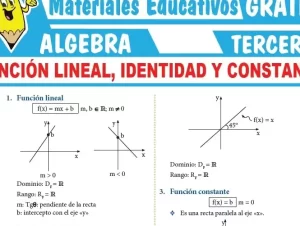
Una función de primer grado, también conocida como función lineal, es una relación matemática que puede expresarse en la forma general de:

[ f(x) = mx + b ]

donde:

• ( m ) representa la pendiente de la línea, que indica la inclinación de la función.

• ( b ) es el intercepto en el eje ( y ), es decir, el valor de la función cuando ( x = 0 ).

Las principales características de una función de primer grado son:

1. Gráfica: La gráfica de una función de primer grado es una línea recta. Esto significa que para cualquier par de valores de ( x ), la función tendrá un único valor correspondiente de ( f(x) ).

2. Dominio y rango: Tanto el dominio como el rango de una función lineal son todos los números reales, lo que significa que puede tomar cualquier valor tanto en su entrada como en su salida.

3. Proporcionalidad: Si la pendiente ( m ) es positiva, la función es creciente; si ( m ) es negativa, la función es decreciente. Si ( m = 0 ), la función se convierte en una constante, y la gráfica sería una línea horizontal.

4. Interceptos: El punto en el que la línea cruza el eje ( x ) (llamado intercepto ( x )) se puede encontrar estableciendo ( f(x) = 0 ) y resolviendo para ( x ).

En resumen, una función de primer grado es una relación lineal que se caracteriza por ser simple de analizar, con comportamientos predecibles y una representación gráfica clara.

¿Cuántos términos tiene una ecuación?

En el contexto de conceptos y definiciones, una ecuación es una expresión matemática que establece la igualdad entre dos cantidades. El número de términos en una ecuación puede variar dependiendo de su naturaleza y complejidad.

Los términos son las partes que conforman la expresión, y pueden ser constantes, variables o el producto de ambas. Por lo general, una ecuación puede tener:

1. Ecuaciones lineales: suelen tener dos o más términos. Por ejemplo, en la ecuación 2x + 3 = 0, hay dos términos en el lado izquierdo.

2. Ecuaciones cuadráticas: generalmente tienen tres términos. Por ejemplo, en x² + 5x + 6 = 0, se presentan tres términos.

3. Ecuaciones polinómicas: pueden tener múltiples términos, dependiendo del grado del polinomio.

En resumen, el número de términos en una ecuación puede ser variable y depende de la estructura específica de la misma.

Preguntas Frecuentes

¿Qué es el concepto de primer miembro en matemáticas y cómo se aplica?

El concepto de primer miembro en matemáticas se refiere a la primera parte de una relación o ecuación, generalmente el valor que se compara con otro. Se utiliza comúnmente en el contexto de proporciones y igualdades, donde el primer miembro es el valor del cual se parte para establecer una relación con el segundo miembro. Por ejemplo, en la ecuación 3 + x = 7, el primer miembro es 3 + x, que se iguala al segundo miembro 7 para resolver la incógnita x.

¿Cuál es la importancia del primer miembro en una ecuación matemática?

El primer miembro de una ecuación matemática es fundamental porque establece la base sobre la cual se iguala el segundo miembro. Su correcto planteamiento asegura que las operaciones y transformaciones posteriores sean válidas, permitiendo resolver la ecuación de manera precisa. Además, el primer miembro ayuda a definir el resultado esperado y orienta el propósito de la ecuación en contextos matemáticos y aplicados.

¿Cómo se determina el primer miembro en una fórmula matemática específica?

El primer miembro en una fórmula matemática se determina identificando la parte de la ecuación que se encuentra a la izquierda del signo de igualdad. Este miembro generalmente representa el resultado o la expresión dependiente, mientras que el segundo miembro (a la derecha del signo) muestra las condiciones o variables que lo afectan.

¿Existen ejemplos concretos que ilustren el primer miembro en matemáticas?

Sí, existen ejemplos concretos que ilustran el primer miembro en matemáticas. Por ejemplo, en una ecuación como x + 5 = 10, el primer miembro es la expresión que se encuentra a la izquierda del signo igual, es decir, x + 5. Otro ejemplo es en una función lineal como f(x) = 2x + 3, donde el primer miembro es 2x + 3.

En conclusión, el concepto de primer miembro es fundamental para comprender diversas estructuras matemáticas y sus aplicaciones. Su adecuada interpretación facilita el análisis de problemas complejos en diferentes ramas de las matemáticas. Te invitamos a compartir este contenido y a seguir explorando más definiciones y conceptos en nuestros próximos artículos.