Concepto De Rotación En Matemáticas: Definición y Aplicaciones Prácticas

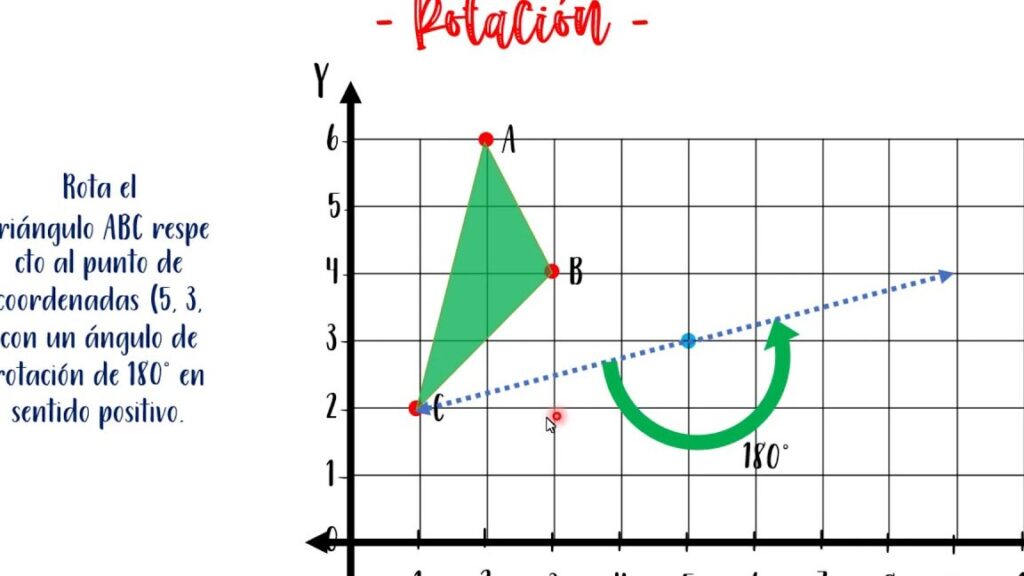
El concepto de rotación en matemáticas se refiere a la transformación geométrica que gira un objeto alrededor de un punto fijo, conocido como el centro de rotación. Esta operación es fundamental en diversas ramas de la geometría, así como en el análisis de simetrías y en la representación gráfica de figuras en un plano. La rotación puede ser medida en grados o radianes y se caracteriza por su ángulo, que determina la cantidad de giro.

Comprender la rotación es esencial no solo para resolver problemas en matemáticas puras, sino también en aplicaciones prácticas como la física, la ingeniería y la informática gráfica. A lo largo de este artículo, exploraremos en profundidad las propiedades, fórmulas y ejemplos relevantes sobre este concepto. Te invitamos a continuar leyendo para profundizar en esta interesante temática.

Entendiendo el Concepto de Rotación en Matemáticas: Definición, Aplicaciones y Ejemplos Prácticos

El concepto de rotación en matemáticas se refiere a una transformación geométrica que implica el giro de un objeto alrededor de un punto fijo, conocido como el centro de rotación. Este proceso es fundamental para entender la simetría, los movimientos en el plano y diversas aplicaciones en la física, la ingeniería y la computación gráfica.

Definición de Rotación

En términos matemáticos, una rotación se puede definir formalmente como una función que mapea cada punto en el plano a otro punto en el mismo plano, manteniendo la distancia desde el centro de rotación y el ángulo de giro. La rotación se caracteriza por:

• Centro de rotación: El punto alrededor del cual se realiza la rotación.
• Ángulo de rotación: La medida del giro, generalmente expresada en grados o radianes.
• Sentido de rotación: Puede ser en sentido horario o antihorario.

La rotación de un punto ((x, y)) alrededor del origen por un ángulo (theta) se puede representar matemáticamente mediante las siguientes fórmulas:

• Rotación antihoraria:
  
  Para un ángulo (theta):
  
  (x’ = x cdot cos(theta) – y cdot sin(theta))
  
  (y’ = x cdot sin(theta) + y cdot cos(theta))
• Rotación horaria:
  
  Para un ángulo (theta):
  
  (x’ = x cdot cos(-theta) – y cdot sin(-theta))
  
  (y’ = x cdot sin(-theta) + y cdot cos(-theta))

Aplicaciones de la Rotación

El concepto de rotación tiene múltiples aplicaciones en diferentes campos, entre las cuales se destacan:

• Geometría: En geometría, la rotación se utiliza para crear figuras simétricas y estudiar sus propiedades.
• Física: En dinámica, la rotación es esencial para describir el movimiento de objetos que giran, como planetas o ruedas.
• Ingeniería: En ingeniería mecánica, el análisis de sistemas rotacionales es crucial para el diseño de maquinaria y mecanismos.
• Computación Gráfica: En gráficos por computadora, la rotación se utiliza para manipular modelos 3D y animaciones.

Ejemplos Prácticos de Rotación

Para ilustrar el concepto de rotación, consideremos los siguientes ejemplos prácticos:

• Rueda de bicicleta: Al girar la rueda, cada punto en su circunferencia rota alrededor del eje central.
• Un reloj: Las manecillas del reloj giran alrededor del centro, creando un movimiento circular
• Juegos de video: La rotación de personajes o cámara en un entorno tridimensional se logra mediante transformaciones de rotación.

La comprensión de la rotación es fundamental para la resolución de problemas y el análisis en diversos contextos científicos y matemáticos, permitiendo una mejor visualización de los fenómenos que involucran movimiento y cambio de posición.

Rotación Geométrica. Con regla y transportador.

TRASLACIONES Y ROTACIONES BÁSICA PRIMARIA.

La Rotación en el Plano Bidimensional

Definición y Propiedades de la Rotación

La rotación en un plano bidimensional se refiere a una transformación geométrica que gira un objeto alrededor de un punto fijo, conocido como el centro de rotación. Este proceso implica cambiar la posición de cada punto del objeto manteniendo su forma y tamaño. La magnitud de la rotación se mide en grados o radianes, y se puede describir usando un ángulo específico.

Una de las propiedades fundamentales de la rotación en el plano es que conserva la distancia entre los puntos. Esto significa que si un punto A se rota a una nueva posición A’, la distancia entre A’ y cualquier otro punto B no se verá alterada. Además, la rotación también conserva los ángulos, lo que permite mantener la similitud entre figuras antes y después del proceso de rotación.

En términos de coordenadas, si un punto P(X, Y) se rota en torno al origen (0, 0) con un ángulo θ, sus nuevas coordenadas P'(X’, Y’) se calculan utilizando las fórmulas:

• X’ = X * cos(θ) – Y * sin(θ)
• Y’ = X * sin(θ) + Y * cos(θ)

Estas fórmulas son esenciales para entender cómo se comportan los puntos en una rotación.

Aplicaciones de la Rotación en Matemáticas y Ciencias

La rotación tiene múltiples aplicaciones tanto en matemáticas puras como en diversas disciplinas científicas. Por ejemplo, en geometría, se utiliza para resolver problemas relacionados con simetría y congruencia. Las figuras rotacionales son fundamentales en la creación de patrones y en la identificación de formas.

En el campo de la física, la rotación es crucial para el estudio del movimiento de los cuerpos. La rotación de planetas y satélites, así como la dinámica de sistemas en rotación, son ejemplos de cómo se aplica este concepto. La comprensión de la rotación también es esencial en la ingeniería, donde el diseño de mecanismos giratorios necesita precisión en la rotación de componentes.

Además, en informática, la rotación se utiliza en gráficos por computadora. Al renderizar imágenes en tres dimensiones, se aplican transformaciones de rotación para mostrar objetos desde diferentes perspectivas y ángulos. Esto es fundamental en el desarrollo de videojuegos y simulaciones visuales.

Rotación y Transformaciones Geométricas

Tipos de Transformaciones Geométricas

Las transformaciones geométricas son herramientas clave en la geometría que permiten manipular figuras en el espacio. Existen varios tipos de transformaciones, entre las que se encuentran la traslación, la reflexión y la rotación. Cada una de estas transformaciones tiene propiedades únicas que afectan la manera en que las figuras se representan.

La traslación implica mover una figura de un lugar a otro sin cambiar su forma ni orientación. Por otro lado, la reflexión se realiza sobre una línea de simetría, creando un espejo de la figura original. La combinación de estas transformaciones, junto con la rotación, proporciona un enfoque integral para comprender la geometría de las figuras en el espacio.

Entender cómo interactúan estas transformaciones es fundamental para resolver problemas complejos en matemáticas. Al aplicar una secuencia de transformaciones, se pueden obtener nuevas figuras y soluciones a diversos problemas geométricos.

Relación entre Rotación y Simetría

La simetría es una característica que juega un papel crucial en el análisis de figuras geométricas. La rotación está intrínsecamente relacionada con la simetría, ya que una figura que tiene simetría rotacional puede ser superpuesta sobre sí misma al ser rotada hasta cierto ángulo. Por ejemplo, un círculo tiene simetría rotacional infinita, lo que significa que puede girar en cualquier ángulo y su forma permanecerá inalterada.

Al estudiar la rotación, se pueden identificar líneas y puntos de simetría dentro de diversas figuras, lo que facilita el análisis estructural en geometría. En contextos educativos, la simetría rotacional a menudo se utiliza para enseñar conceptos básicos de rotación de manera más comprensible.

La relación entre rotación y simetría también se encuentra en diversas áreas de arte y arquitectura, donde se emplean patrones rotacionales para crear composiciones estéticamente agradables. Este enfoque no solo añade belleza sino que también puede influir en la funcionalidad de las estructuras.

Matemáticas de la Rotación en el Espacio Tridimensional

Extensión del Concepto de Rotación al Espacio

Mientras que la rotación en el plano bidimensional se centra exclusivamente en dos dimensiones, el concepto se complica al extenderse al espacio tridimensional. Aquí, la rotación se define en torno a un eje, que puede ser cualquiera de los ejes coordenados: X, Y o Z. Esta complejidad adicional permite una mayor variedad de movimientos y transformaciones.

Los objetos en el espacio tridimensional pueden rotar en múltiples direcciones al mismo tiempo. Los ángulos de rotación se miden en términos de ángulos de Euler o mediante cuaterniones, que son herramientas matemáticas que simplifican el cálculo y la representación de rotaciones. Esto es especialmente útil en campos como la robótica y la animación por computadora, donde es esencial representar correctamente la orientación de objetos tridimensionales.

La capacidad de rotar objetos en el espacio tridimensional amplía significativamente las aplicaciones del concepto de rotación y proporciona un marco para resolver una variedad de problemas complejos en ingeniería y física.

Ejemplos Prácticos de Rotación en el Espacio

En el ámbito de la ingeniería, la rotación se aplica a estructuras arquitectónicas que requieren ser soportadas bajo diferentes cargas. Los ingenieros utilizan principios de rotación para diseñar componentes que deben resistir fuerzas en diversas direcciones.

En la aeroespacial, la rotación es vital para el movimiento de aeronaves y naves espaciales. El control sobre la rotación permite a estas máquinas maniobrar y estabilizarse durante el vuelo, asegurando que puedan realizar giros y ajustar su orientación adecuadamente.

Finalmente, en la realidad virtual y aumentada, las transformaciones de rotación son esenciales para crear entornos inmersivos y dinámicos. Las tecnologías que permiten que los usuarios interactúen con objetos virtuales dependen de algoritmos de rotación precisos para asegurar que la percepción visual sea coherente y realista.

Preguntas Frecuentes

¿Qué es el concepto de rotación en matemáticas?

El concepto de rotación en matemáticas se refiere al movimiento de un objeto alrededor de un punto fijo, conocido como centro de rotación. Este movimiento se describe en términos de un ángulo de rotación, que indica cuánto se ha girado el objeto en grados o radianes. En geometría, la rotación es una transformación que cambia la posición de los puntos de un plano sin alterar su forma ni tamaño.

¿Cuáles son las propiedades de la rotación en un plano cartesiano?

Las propiedades de la rotación en un plano cartesiano son:

1. Centro de rotación: La rotación se realiza alrededor de un punto fijo, conocido como el centro de rotación.
2. Ángulo de rotación: Se determina el ángulo en grados o radianes que especifica cuánto se gira un punto.
3. Sentido de rotación: Puede ser horario o anti-horario, influenciando la dirección del giro.
4. Distancia fija: Todos los puntos rotan a una distancia constante del centro de rotación.
5. Invariancia de distancia: Las distancias entre los puntos no cambian tras la rotación, manteniéndose en su posición relativa.

Estas propiedades son fundamentales para entender cómo las figuras se transforman en un plano al aplicar rotaciones.

¿Cómo se representa una rotación en coordenadas polares?

En coordenadas polares, una rotación se representa modificando el ángulo (theta) de un punto. Si un punto está en la posición ((r, theta)), tras una rotación de un ángulo (phi), su nueva posición será ((r, theta + phi)). Así, se mantiene la distancia radial (r) y se ajusta el ángulo (theta).

¿Qué aplicaciones tiene el concepto de rotación en geometría y álgebra?

El concepto de rotación en geometría y álgebra tiene diversas aplicaciones. En geometría, se utiliza para transformar figuras en el plano, permitiendo análisis de simetrías y patrones. En álgebra, se aplica en matrices de transformación para representar rotaciones, facilitando la resolución de problemas relacionados con coordenadas y vectores. Además, es esencial en áreas como la animación por computadora y la robótica, donde se requiere un control preciso del movimiento.

En conclusión, la rotación es un concepto fundamental en matemáticas que permite comprender diversas transformaciones geométricas. Su estudio posibilita la aplicación en múltiples áreas, desde la física hasta el arte. Te invitamos a compartir este contenido y a seguir explorando otros conceptos relevantes en nuestras próximas publicaciones.